第4回: 加算器(その2)
桁上げ先見加算器(p.138)
前回みたように、全加算器の論理式は、
キャリーが生成する場合(生成項)と伝播する場合(伝播項)に分けて、
次のように書くことができました。
- Gn = An・Bn (生成項)
- Qn = An
Bn (伝播項)
- Cn = Gn + Qn・Cn-1 (生成項=1または「伝播項=1かつCn-1=1」のとき、Cn=1)
(または Pn = An + Bn とおいて、Cn = Gn + Pn・Cn-1)
たとえば4ビット加算器をつくるとして、
この生成項と伝播項を順番に書くと次のようになります。
| G0 = A0・B0 | Q0 = A0B0 |
C0 = G0 + Q0・C-1 |
| G1 = A1・B1 | Q1 = A1B1 |
C1 = G1 + Q1・C0 |
| G2 = A2・B2 | Q2 = A2B2 |
C2 = G2 + Q2・C1 |
| G3 = A3・B3 | Q3 = A3B3 |
C3 = G3 + Q3・C2 |
このうち、C1は次のように書くことができます。
C1 = G1 + Q1・C0 = G1 + Q1・(G0 + Q0・C-1)
= A1・B1 + (A1B1){A0・B0 + (A0B0)・C-1}
つまり、C1が、前の桁からの桁上がりC0を使わずに、
入力An, Bn(とC-1)のみであらわせることになります。
同様に、C2, C3も、入力An, Bnのみであらわすことができます。
- C2 = G2 + Q2・C1 = G2 + Q2・(G1 + Q1・C0)
= G2 + Q2・(G1 + Q1・(G0 + Q0・C-1))
= G2 + Q2・G1 + Q2・Q1・G0 + Q2・Q1・Q0・C-1
- C3 = G3 + Q3・(G2 + Q2・(G1 + Q1・(G0 + Q0・C-1)))
= G3 + Q3・G2 + Q3・Q2・G1 + Q3・Q2・Q1・G0 + Q3・Q2・Q1・Q0・C-1
ちなみにSn = Qn + Cn-1ですから、
これらを使うと、この4ビット加算器の回路図は次のようになります。
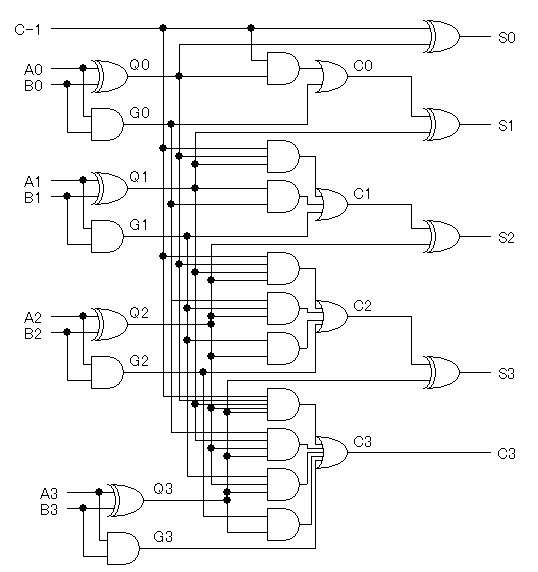
この構成では、RCAのようなキャリーの伝播は起こらず、
すべての桁のキャリーが、入力An, Bnのみから決まるため、
RCAのように桁数に比例した演算時間がかかることはありません。
このような構成の加算器を
キャリー先見加算器 (Carry Look-ahead Adder; CLA)
と呼びます。
このようにCLAは桁数が多くても高速な演算が可能ですが、
桁数が多くなるほど、キャリーCnを求めるための論理式が
急激に複雑になり、論理回路が大規模になってしまうという問題があります。
(元気がある人は8ビットCLAでも作ってみましょう・・・)
2進桁上げ先見加算器(p.141)
ビット数が多い加算器をつくるときに
さらに高速化が可能な構成として、
2進桁上げ先見加算器(Binary Carry Look-ahead Adder; BCLA)というものが
あります。
これはかなり大変ですので、気合を入れていきましょう。
- Gn = An + Bn (生成項)
- Qn = An Bn (伝播項)
- Cn = Gn + Qn・Cn-1
- Sn = An Bn Cn-1
= Qn Cn-1
ですが、このCn = gn + qnとおいてみると、
次のように書くことができます。
- Cn = Gn + Qn・(gn-1 + qn-1) = (Gn + Qn・gn-1) + Qn・qn-1
= gn + qn
つまり、(gn, qn)は、(Gn, Qn), (gn-1, qn-1)から、この式のように
求められる、というわけです。これを「◎」という「演算」として
定義することにしましょう。
つまり、
- (gn, qn) = (Gn, Qn)◎(gn-1, qn-1)
さてC-1 = G-1 + Q-1・C-2のはずですが、C-1=0(最初の桁には、下の桁からの
桁上がりはない)のはずです。
ところがG-1 = Q-1 = 0 (最初の桁には、キャリーの生成も伝播もない)なので、
C-2は0でも1でも構いません。そこでC-2=1、とおくことにしましょう。
そうすると、(g-1, q-1)は次のように求められます。
- C-1 = G-1 + Q-1・C-2 = G-1 + Q-1 = g-1 + q-1
→よって、g-1 = G-1, q-1 = Q-1
これを使うと、(gn, qn)が、次のように順番に求められることになります。
- (g0, q0) = (G0, Q0)◎(g-1, q-1) = (G0, Q0)◎(G-1, Q-1)
- (g1, q1) = (G1, Q1)◎(g0, q0) = (G1, Q1)◎(G0, Q0)◎(G-1, Q-1)
- (g2, q2) = (G2, Q2)◎(g1, q1) = (G2, Q2)◎(G1, Q1)◎(G0, Q0)◎(G-1, Q-1)
- ...
ちなみにn桁目のキャリーCnとn桁目の和Snは、次のように求められます。
- Cn = gn + qn
- Sn = An Bn Cn-1
= Qn Cn-1
これを使うと、たとえば8桁の加算器を次のように構成することができるでしょう。
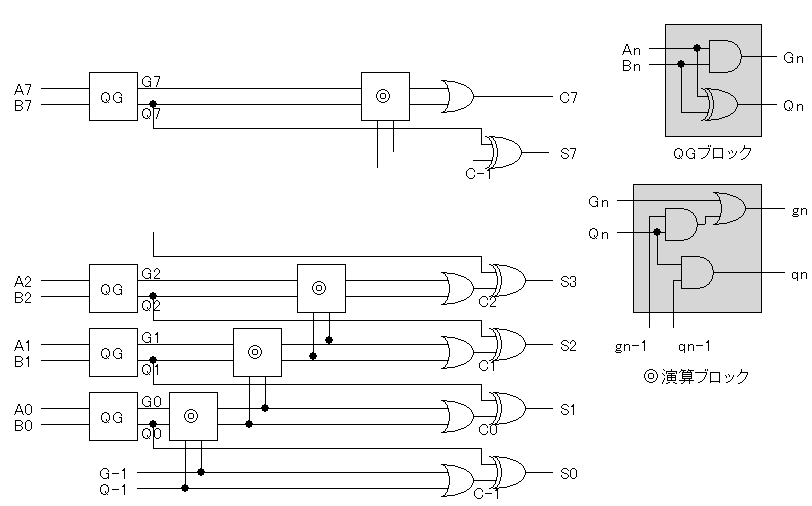
ここでは、◎演算を行う部分と、最初にGnとQnと生成する部分を
まとめて機能ブロックとして描いてあります。
ただしこれだと、8桁目の結果が出るまでに、◎演算を7回も行う必要があり、
あまり高速とは言えません。
そこで、◎演算の順番を変えていいことに注目すると、
要は右端の(gn, qn)に至るまでに、(G0, Q0), (G1, Q1), ..., (Gn, Qn)の
◎演算を通ればいいことになりますから、次のように考えることができます。
- (g0, q0) = (G0, Q0)◎(G-1, Q-1)
- (g1, q1) = (G1, Q1)◎(G0, Q0)◎(G-1, Q-1)
- (g2, q2) = (G2, Q2)◎(G1, Q1)◎(G0, Q0)◎(G-1, Q-1)
- (g3, q3) = (G3, Q3)◎(G2, Q2)◎(G1, Q1)◎(G0, Q0)◎(G-1, Q-1)
- (g4, q4) = (G4, Q4)◎(G3, Q3)◎(G2, Q2)◎(G1, Q1)◎(G0, Q0)◎(G-1, Q-1)
- ...
これをうまく使うと、うまいことを思いつく人がいるものだ、と
感心するしかありませんが、次のような回路で、8ビットの加算器を
つくることができることになります。
たとえば(g4, q4)を生成するためには、(G4, Q4)から(G-1, Q-1)までの
◎演算をとればよいわけですが、図の赤矢印のように、
たしかにこれらすべてが◎演算をとおっています。
このような構成の加算器を
2進桁上げ先見加算器(BCLA)と呼びますが、
一般に、2Mビットの加算器をつくるのに、
M段の◎演算ブロックを通ることになるため、
劇的な高速化が可能となります。
(2004.10.25)この図は一部間違いがあります。
正しくはこちらを参照してください。
このような、「規則的な構造(アーキテクチャ)」は、
一見複雑そうでも、集積回路を作るときには、
要素回路をただ並べるだけなので、実は非常に楽チンで効率的なのです。
この回のソボクな疑問集
戻る