第6回: 加算器(その4) / ALU(その1)
桁上げ保存加算器(p.140)
趣向を変えて、2つ以上の数の加算を行う加算器を
考えてみましょう。(これは実は後ほど乗算器のところでで使います)
例えば、4ビットの3つの数 X={X3, X2, X1, X0}, Y={Y3, Y2, Y1, Y0},
Z={Z3, Z2, Z1, Z0}を加算する加算器を考えてみます。
順当には、まずはX+Yを4ビット加算器で求め、
その結果とZの和を、さらに別の4ビット加算器で求めれば
よいわけですが、ちょっと工夫をすると、次のような回路構成を
とることができます。
つまりまずX+Y={C'3, S'3, S'2, S'1, S'0}をもとめ、
続いて、それとZとの和を求めているように見えますが、
実はX+Yの加算のところで、上の桁の和は求められていません。
(例えば、本来はS'1 = X1 + Y1 + C0のはずだが、C0が入ってきていない)
つまり下の桁からの桁上がりを加算しないまま、Zを足してしまっているわけです。
どうせここでも桁上がりが発生するだろうから、
X+Yのところで桁上げを求めずに、Zを足した後で、桁上げを
まとめて求めているわけです。
最後の桁上げを求める段を、この回路構成では桁上げ伝播加算器(RCA)を
使っていますが、もちろんCLAやBCLAでも構いません。
種々の加算器の比較
これまで、全加算器自体や、それを使った、RCAやCLA、BCLAなどの
多ビットの加算器の構成を見てきましたが、
最後に比較の一例を紹介しておきましょう。
もちろん加算器の速度などは、設計するときのテクノロジ(最小加工寸法など)に
依存しますので、あくまでもこれは一例ですが、
傾向は、テクノロジが変わってもそうは変わらないでしょう。
これからわかるように、RCAのほうが遅いがやや回路規模は小さい、
というところでしょうか。
実際には、要求される演算速度、回路規模、消費電力などから
適切な構成を選択することになります。
※RCAのMOSFET数が妙に多いように見えますが、
この「MOSFET数」は、標準サイズのMOSFETに換算した数です。
(つまり実際のLSI上で占める面積の目安)
高速化するためにMOSFETの大きさを大きくしないといけない部分が
多く、MOSFETの数自体は少ないものの、この換算した「MOSFET数」は
多くなるわけです。
算術論理演算ユニット(ALU)
1の補数と2の補数
2進数で負の数をあらわすときには、「2の補数」というものを
使うのでした。
「2の補数」は、「1の補数(全ビットのNOTをとったもの)」+1で、
次の表のように、たしかに足してゼロになる(最上位の桁上がりは無視する)
ので、負の数をあらわしていることがわかります。
| 数(1) | 1の補数 | 2の補数(2) | (1)+(2) |
| 000 | 111 | (1)000 | (1)000 |
| 001 | 110 | 111 | (1)000 |
| 010 | 101 | 110 | (1)000 |
| 011 | 100 | 101 | (1)000 |
| 100 | 011 | 100 | (1)000 |
| 101 | 010 | 011 | (1)000 |
| 110 | 001 | 010 | (1)000 |
| 111 | 000 | 001 | (1)000 |
加算器を使った減算器
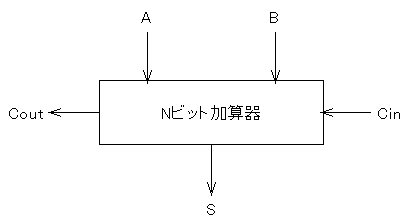この2の補数を使うと、減算を行う減算器を作ることができます。
つまりこのようにN桁の加算器で、最下位の桁上がり入力Cinを
使うと、S = A + B + Cin ということですが、
たとえばBのところに/B(つまりBの全ビットの反転をとったもの)を
入力し、Cin=1とすれば、S = A + (/B + 1) となりますが、
「/B+1」は、Bの2の補数そのものですから、結果としてS = A - B を
求めたのと同じことになります。
このように拡張していくと、B, Cinに与える値によって
次の8通りの演算ができることがわかります。
| S1 | S0 | B | Cin | S = A + B + Cin | 内容 |
| 0 | 0 | すべて0 | 0 | A | そのまま |
| 0 | 0 | すべて0 | 1 | A+1 | increment |
| 0 | 1 | B | 0 | A+B | 加算 |
| 0 | 1 | B | 1 | A+B+1 | |
| 1 | 0 | /B | 0 | A+/B | |
| 1 | 0 | /B | 1 | A+/B+1 = A-B | 減算 |
| 1 | 1 | すべて1 | 0 | A -1 | decrement |
| 1 | 1 | すべて1 | 1 | A | |
つまりBから、選択信号(S1, S0)によって、すべて0, B, /B, すべて1、の
いずれかをつくり、それとCin、AをNビット加算器に加えれば、
これらのすべての算術演算を行うことができるわけです。
ちなみにBのところは、上のような回路(EXORゲートそのもの)を入れておけば、
f=0のときはBが、f=1のときは/Bが、加算器に与えられることになりますから、
fの値に応じて加算(f=0)と減算(f=1)を切り替えるためには
次のような回路とすればよいでしょう。
このように、いろいろな演算機能をもつ演算ユニットを総称して
算術論理演算ユニット (Arithmetic Logic Unit; ALU)と
呼びますが、この回路は、加算と減算機能をもつALU、ということになります。
この回のソボクな疑問集
戻る