第7回: ALU(その2)
論理演算ユニット
ALUは、加算減算のような算術演算だけでなく、
論理演算、すなわちビットごとの論理積(AND)・論理和(OR)・否定(NOT)
・排他的論理和(EXOR)も演算できる必要があります。
おそらく最も素直な論理演算ユニットの作り方は、
次のようなものでしょう。
つまり4種類の演算を、それぞれ論理ゲートで用意しておいて、
その中から希望のものをS1, S0の値の組でどれかが選ばれるセレクタで選んで
出力とする、ということです。
ただ、これはあまり格好いい回路とはいえません。
そこで、このALUの真理値表を書いてみることにしましょう。
A | 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
B | 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
S1 | 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
S0 | 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
---+---------------------------------------
X | 0 1 1 1 0 0 0 1 0 1 1 0 1 0 1 0
(OR) (AND) (EXOR) (NOT)
そしてこの真理値表から、積和標準形やカルノー図などを用いて論理式を
つくり、それから論理回路をつくれば、所望の論理演算ユニットを
つくることができます。
(つまり入力がA, B, S1, S0の4変数で、出力がXの論理式)
最も素直なALUの構成
さてALUは、算術論理演算ユニットというくらいですから、
算術演算(加減算)と論理演算を両方ともできなければいけません。
算術演算は前回つくりましたし、論理演算はいま作りましたから、
この2つを組み合わせて、次のようにセレクタでどちらかを選べば、
ALUが完成することになります。
ただし、これも先ほどのセレクタを使った論理演算器と同様、
あまり格好いい回路とはいえません。
加算器をベースとしたALUの構成
前回つくった、S1, S0でいろいろな演算を選べる算術演算回路で、
各桁ごとに独立に演算をする(つまり下の桁のキャリーは入らず、
次の桁へキャリーを伝えない)ことを考えましょう。
すると各桁の加算の結果は、S = A + B + Cinですが、
Cin=0とすれば、S = A + B (算術和)、つまりS = A
B
(排他的論理和)となります。
これに、前回の(S1, S0)によってBから「すべて1」などを
作る機能ブロックを通したあとのBを加えるとすると、
(S1, S0)の値によって次のような演算が行われることになります。
| S1 | S0 | A | B | X = AB | 演算 |
| 0 | 0 | A | 0 | A | そのまま |
| 0 | 1 | A | B | AB | EXOR |
| 1 | 0 | A | /B | A/B | EXNOR |
| 1 | 1 | A | 1 | /A | NOT |
このように、EXORとNOTはすでに得られていますから、
残りのANDとORを考えてみましょう。
OR演算
(S1, S0) = (0, 0)のとき、AそのものがXであったわけですが、
このAの代わりに「A + B」(AとBの論理和)を与えることを考えてみましょう。
つまりあの演算回路の入力Aのところに、1つORゲートを置くわけです。
すると、このときのXは、X = A + B と、論理和が求められることになります。
AND演算
(S1, S0) = (1, 0)のとき、AとBのEXNOR、つまり X = A・B + /A・/Bが
得られています。
そこで、やや天下り的なのですが、Aの代わりに「A + K」(AとKの論理和)
を与えることを考えてみましょう。
つまりあの演算回路の入力Aのところに、1つORゲートを置くわけです。
すると、このときのXは、次のようになります。
- X = (A + K)・B + /(A + K)・/B = A・B + K・B + /A・/B・/K
ここで、K=/Bとしてみましょう。
すると、K・B = /B・B = 0で、/A・/B・/K = /A・/B・B = 0 となり、
X = A・B となってしまいます。
つまり、(S1, S0) = (1, 0)のときに、Aの代わりに「A+/B」をAに
与えれば、出力Xは論理積A・Bとなる、というわけです。
加算器をベースとしたALU
もう1つの機能選択信号S2を用意し、
- S2 = 0 のときは、算術演算回路
- S2 = 1 のときは、論理演算回路
となるようにしてみましょう。
つまり次のような機能ですが、ここまで見てきたことを総合すると、
特に論理演算を行うときには、A, Bをそれぞれ次のようなものに
代える必要があります。
| S2 | S1 | S0 | Cin | A | B | X | 演算 |
| 0 | 0 | 0 | 0 | A | 0 | A | そのまま |
| 0 | 0 | 0 | 1 | A | 0 | A+1 | increment |
| 0 | 0 | 1 | 0 | A | B | A+B | 加算 |
| 0 | 0 | 1 | 1 | A | B | A+B+1 | |
| 0 | 1 | 0 | 0 | A | /B | A-B-1 | |
| 0 | 1 | 0 | 1 | A | /B | A-B | 減算 |
| 0 | 1 | 1 | 0 | A | 1 | A-1 | decrement |
| 0 | 1 | 1 | 1 | A | 1 | A | そのまま |
| 1 | 0 | 0 | 0 | A+B | 0 | A+B | 論理和(OR) |
| 1 | 0 | 1 | 0 | A | B | AB | 排他的論理和(EXOR) |
| 1 | 1 | 0 | 0 | A+/B | /B | AB | 論理積(AND) |
| 1 | 1 | 1 | 0 | A | 1 | /A | 否定(NOT) |
さてこのようなA, Bと、1桁分の下の桁からのキャリーCinは、(S2, S1, S0)に応じて、それぞれ次のように代わります。
- A : S2=0のときはA。S2=1のとき、 S1=S0=0→A+B、S1=1,S0=0→A+/B
- B : (S2に無関係)、S1=S0=0→0, S1=0,S0=1→B, S1=1,S0=0→/B, S1=S0=1→1
- Cin : S2=0のときCin(下の桁のCout)、S2=1のとき0
全体としては、次の図のような構成をとって、
A, B, Cinを、S2〜S0の値に応じて変える、と考えるとよいでしょう。(1ビット分)
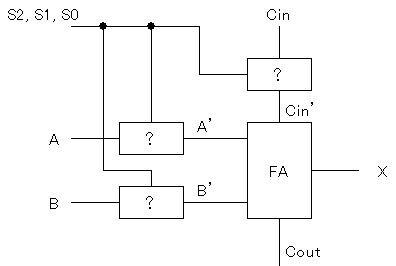
これから、1ビット分の加算器のA, B, Cinに与えるべき
A', B', Cin'は次のような論理式となるでしょう。
- A' = A + S2・/S1・/S0・B + S2・S1・/S0・/B
- B' = S0・B + S1・/B
- Cin' = /S2・Cin
これをそのまま論理回路にして、全加算器につなげてあげれば、
本物のALUが完成することになります。
課題2
この方法で、機能が(S2, S1, S0)で上記のように選ばれる2ビットのALUを
設計し、その過程と論理回路図を示してください。
なお全加算器はブロック図のままで構いません。
また多ビット加算器の構成はRCAで構いません。
- 提出方法：レポート用紙(できればA4版)に、名前、学科、名列番号を明記の上、上記内容の解を、328室前のレポートBOXまで
- 期限：11/25(木)18:00
- 注意：誰かと相談した場合や、書籍やWebページなどを参考にした場合は、
その旨(出典)を明記すること
解答例
この回のソボクな疑問集
戻る