第8回: 乗算器(その1)

今回から3回ほどにわたって、掛け算をする回路、つまり乗算器についてみていきましょう。もちろん乗算は加算の繰り返しですが、非常によく使う演算なので、乗算器自体に関して、いろいろな工夫が知られています。

2進数の乗算(p.155)

乗算の基本は、やはり筆算です。例えば4桁の2進数の掛け算「1001×0101」(10進数で、9×5=45)を次のように求めることができるでしょう。

    1001  ：被乗数(X)
×) 0101  ：乗数  (Y)
----------
    1001  ：部分積
   0000
  1001
 0000
---------
 0101101 (0x2d = 45(dec))

乗数Yの各桁に対して、被乗数Xを順番にずらして並べていき、最後にすべてを足すわけですが、途中の、被乗数Xを順番にずらしていった項を 部分積と呼びます。部分積を求めるのは簡単で、被乗数Yの、その桁が1であればXそのもも、その桁が0であれば0、となります。

一般に、N桁の被乗数Xと乗数Yを、次のように表現することにしましょう。

X = ∑_n=0^N-1 x_n・2ⁿ
Y = ∑_n=0^N-1 y_n・2ⁿ

つまり最上位ビット(MSB)がx_N-1, y_N-1で、最下位ビット(LSB)がx₀, y₀とするわけです。これを使うと、XとYの積Zは、次のように書くことができるでしょう。

Z = X・Y = (∑_n=0^N-1 x_n・2ⁿ) ・(∑_m=0^N-1 y_m・2^m) = ∑_m=0^N-1{ ∑_n=0^N-1 (x_n・y_m)}2^n+m

ちなみに筆算で書くと、例えば4桁の場合だとこんな感じです。

                                  x3      x2       x1     x0    被乗数X
                           ×)    y3      y2       y1     y0    乗数Y
                        ---------------------------------------
                                x3・y0  x2・y0  x1・y0  x0・y0  部分積0
                        x3・y1  x2・y1  x1・y1  x0・y1          部分積1
                x3・y2  x2・y2  x1・y2  x0・y2                  部分積2
        x3・y3  x2・y3  x1・y3  x0・y0                          部分積3
---------------------------------------------------------------
  z7      z6      z5      z4      z3      z2      z1      z0    積Z

並列乗算回路

もっとも直感的な乗算器の作り方は、この筆算をそのまま回路にする、というものです。つまり部分積x_i・y_jを求める回路と、上から下へ部分積を加算していく、という筆算の手順のとおりに並べる、という方法です。

結局1桁の2進数の乗算は、AND演算そのものですから、この図中のBCというブロックのように、部分積x_i・y_jをANDゲートで求めつつ、上から下へ足していく加算を行う回路を並べていけばよいことになります。ちょっと見づらいですが、全体ではキャリー保存加算器(CSA)の構成をとり、最後のキャリーの吸収にはキャリー伝播加算器(RCA)を使っています。このような構成の乗算器を並列乗算回路と呼びます。

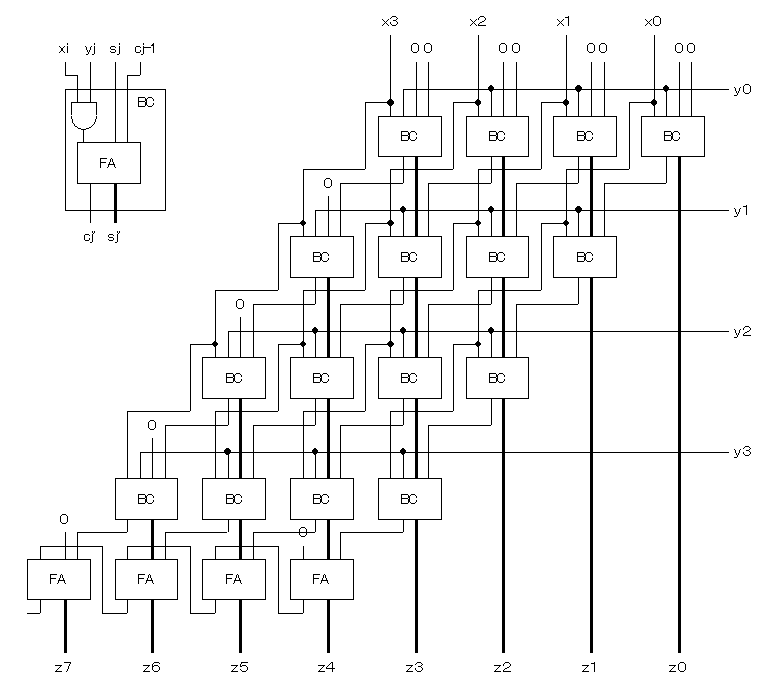
並列乗算回路では、部分積の段数、つまり乗数Yの桁数分だけ BCブロック、つまりほぼ加算器が並びますので、この段数が、全体の演算時間を決めるもっとも大きな要因となります。

ブースのアルゴリズム

乗算器の高速化のためには、部分積の段数を減らすことが効果的ですが、そのためのうまい方法として、ブースのアルゴリズム (Booth's algorithm) というものが知られています。

まず、被乗数Xと乗数Yを、N桁の符号つきの2進数で次のようにあらわすことにします。

X = -1・x_N-12^N-1 + ∑_n=0^N-2 x_n・2ⁿ
Y = -1・y_N-12^N-1 + ∑_n=0^N-2 y_n・2ⁿ

念のため確認しておくと、2の補数で負の数を表すと、例えば3桁の場合、最上位ビットx₂が0の場合と1の場合を並べて比べてみると、次のようになります。

  x2=0(正の数)  x2=1(負の数)
----------------------------
  000 (0)       100 (-4)
  001 (1)       101 (-3)
  010 (2)       110 (-2)
  011 (3)       111 (-1)

つまり最上位ビットx_3-1が0の数から、 -4 = -1・2^3-1をひくと、最上位ビットx_3-1だけを1にした数、になっていますから、先の式のように、「-1・x_N-12^N-1」という項を含めて、負の数と正の数をまとめて表すことができるわけです。

ここで、やや唐突ですが、次のようなY_jを考えましょう。

Y_j = y_2j +y_2j-1 - 2y_2j+1

このようなY_jに対して、次のようにYを求めることにしましょう。

Y = ∑_j=0^(N-2)/2 Y_j・2^2j

たとえばj = 0, 1, 2を順番に足してみる(つまりN=6)と、次のようになります。

Y₀・2⁰ + Y₁・2² + Y₂・2⁴ = (y₀ + y_-1 - 2y₁)・2⁰ + (y₂ + y₁ - 2y₃)・2² + (y₄ + y₃ - 2y₅)・2⁴
= -1・y₅・2⁵ + ∑_n=0⁴ y_n・2ⁿ

ただしy_-1 = 0とおきました。つまり、もともとのYそのものとなるわけです。一応証明しておきましょう。

y_2jの項はY_jのみに含まれ、 Yを求める式ではy_2j・2^2jとなる。
y_2j-1の項は、Y_jとY_j+1に含まれ、 Yを求める式の中で、y_2j-1が出てくる項は次のとおり。
Y_j・2^2j + Y_j+1・2^2(j+1) → (-2y_j+1)・2^2j + y_j+1・2^2(j+1) = y_j+1(2^2j+2-2^2j+1) = y_j+1・2^2j+1
j=(N-2)/2のとき、Y_(N-2)/2の最後には -2y_N-1という項があるが、これが含まれる項は、 -2y_N-1・2^N-2 = -1・y_N-1・2^N-1
以上から、これらをすべて足したものは、Yとなる。

さてこのYの表現を使うと、Z = X・Yは次のように求められます。

Z = X・∑_j=0^(N-2)/2Y_j・2^2j = ∑_j=0^(N-2)/2Z_j (とおくことにする)

ここでZ_jはj段目の部分積で、次のように書くことができます。

Z_j = X・Y_j・2^2j = (-1・x_N-12^N-1 + ∑_n=0^N-2 x_n・2ⁿ) ・(y_2j + y_2j-1 - 2y_2j+1)・2^2j

つまり乗算結果Zを求めるためには、jを0から順に XをY_j・2^2j倍ずつして求めたZ_jを足していけばよいわけです。

ポイントは、この加算が、(N-2)/2回、つまり普通に部分積を足していく場合の半分程度の回数で済む、ということです。これは、y_2j +y_2j-1 - 2y_2j+1という項を使って、1個とばしで部分積を足していく方法、と考えることができます。

このうち、Y_jに含まれる y_2j, y_2j-1, y_2j+1の組み合わせは 8通りしかありませんから、それをまとめると次のようになるでしょう。

y_2j+1 y_2j y_2j-1 Y_j Z_j Z_jを求める作業 Q1 Q2 QN

0 0 0 0 0 何もしない 0 0 0

0 0 1 1 X・2^2j 2j ビットシフト 1 0 0

0 1 0 1 X・2^2j 2j ビットシフト 1 0 0

0 1 1 2 X・2^2j+1 (2j+1)ビットシフト 0 1 0

1 0 0 -2 -X・2^2j+1 (2j+1)ビットシフトし、2の補数 0 1 1

1 0 1 -1 -X・2^2j 2j ビットシフトし、2の補数 1 0 1

1 1 0 -1 -X・2^2j 2j ビットシフトし、2の補数 1 0 1

1 1 1 0 0 何もしない 0 0 0

ここで、Q1, Q2, QNは、Z_jを求める作業で、するべき操作を示す、次のような数値です。

Q1=1のとき、2j ビットシフトする
Q2=1のとき、(2j+1)ビットシフトする
QN=1のとき、シフトし結果の2の補数を求める(=-1をかける)

このように乗算を行う方法を ブースのアルゴリズム (Booth's algorithm)と呼びます。

ここの「ブースのアルゴリズム」の部分の抜粋

この回のソボクな疑問集

戻る

y_2j+1	y_2j	y_2j-1	Y_j	Z_j	Z_jを求める作業	Q1	Q2	QN
0	0	0	0	0	何もしない	0	0	0
0	0	1	1	X・2^2j	2j ビットシフト	1	0	0
0	1	0	1	X・2^2j	2j ビットシフト	1	0	0
0	1	1	2	X・2^2j+1	(2j+1)ビットシフト	0	1	0
1	0	0	-2	-X・2^2j+1	(2j+1)ビットシフトし、2の補数	0	1	1
1	0	1	-1	-X・2^2j	2j ビットシフトし、2の補数	1	0	1
1	1	0	-1	-X・2^2j	2j ビットシフトし、2の補数	1	0	1
1	1	1	0	0	何もしない	0	0	0