第9回: 乗算器(その2)

ブースのアルゴリズム(続き)

前回紹介したブースのアルゴリズムを使って、乗算を実際にやってみましょう。たとえば6桁で、X = -9, Y = +25 の積を求めてみましょう。

まずX, Yを2進数で求めると次のようになります。

X = 11 0111 = x₅x₄x₃x₂x₁x₀
Y = 01 1001 = y₅y₄y₃y₂y₁y₀

いまの場合、N=6ですから、j は0～(N-2)/2、つまり0～2まで求めればよく、Y_jは次のようになるでしょう。

j	y_2j+1	y_2j	y_2j-1	Y_j	Z_j
0	0	1	0	1	X・2⁰
1	1	0	0	-2	-2X・2²
2	0	1	1	2	2X・2⁴

このZ_jをすべて加算すると、次のようになるでしょう。

Z0 =                  11111110111 (11桁にあわせる)
Z1 = -2・  11011100 = 00001001000 (11桁にあわせる)
Z2 =  2・1101110000 = 11011100000
----------------------------------
                      11100011111

この求められた結果は、2進数で2の補数の00011100001 = 225の負の数=-225ですから、たしかに-9×25 = -225となっていることがわかります。

ブースのアルゴリズムを使った乗算器の設計

ブースのアルゴリズムによるQ1, Q2, QNの生成

ブースのアルゴリズムでは、まずY_jの値からZ_jを求めるときに、 Y_jの値、つまりy_2j, y_2j+1, y_2j-1の値に応じて、被乗数Xに対して、2jビットのシフト(Q1)、(2j+1)ビットのシフト(Q2)、 2の補数を求める(QN)、のいずれかの演算を組み合わせて Z_jを求めました。これは、逆に言えばy_2j, y_2j+1, y_2j-1の値の組(8通り)に対して Q1, Q2, QNが0か1かを、組み合わせ論理回路で求めればよいわけです。つまり次のような真理値表の組み合わせ論理回路を求めればよいわけです。

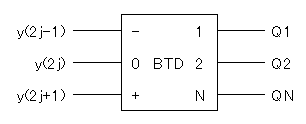
y(2j+1) y(2j) y(2j-1) Y(j) | Q1 Q2 QN
---------------------------+---------
  0       0      0     0   |  0  0  0
  0       0      1     1   |  1  0  0
  0       1      0     1   |  1  0  0
  0       1      1     2   |  0  1  0
  1       0      0    -2   |  0  1  1
  1       0      1    -1   |  1  0  1
  1       1      0    -1   |  1  0  1
  1       1      1     0   |  0  0  0

これから、次のような論理式が導かれるでしょう。

Q1 = y_2jy_2-1
Q2 = (y_2j+1y_2j)・/(y_2jy_2j-1)
QN = y_2j+1・/(y_2j・y_2j-1)

この論理回路を、BTDセルと名づけて、次のような記号でかくことにしましょう。

(ブースのアルゴリズムを使った乗算器の続きは次回へ)

ここの「(続)ブースのアルゴリズム」の部分の抜粋

この回のソボクな疑問集

戻る