第2回分
CLAで生成項と伝播項以外の組み合わせはあるのか?
CLAの考え方は、生成項と伝播項を使おう、というものですから、
それ以外はない、という言い方もできると思います。
Gn,Qnは半加算器と同じ論理式なので、それを利用できないか?
まさにそのとおりです。
CLAは回路が複雑化しやすいが、電力も大きくなるか?
回路の動作割合(主に、動作時に出力の値が変化する割合)が
どのゲートでもほぼ同じであれば、消費電力は回路規模に
ほぼ比例するといえます。
CLA、RCAの桁数はどこまで増やせるのか?
CLA、RCAの桁数を増やしすぎると何か問題は起こらないか?
CLA単体は講義で述べたとおり4桁程度が現実的で、
RCAは、回路規模と遅延時間が許される範囲であれば何桁でも、でしょうね。
CLA、RCAの桁数を極限までもっていくとどちらが高速か?
なかなか面白い点だと思います。
RCAでも、桁数によっては、うまくつくるとCLAを組み合わせたものより
高速になる可能性はあります。
その話は、次回に。
5桁以上のCLAは作れないのか?
作ることはできますが、あまり実用的ではない(回路規模が大きく、
速度が期待するほど速くならない)、ということです。
桁数が少ないとき(2桁など)、CLAはRCAよりも早いのか?
2桁ぐらいならば、ほとんど同じなのではないでしょうか。
C-1は必要なのか?
便宜上、ですね。
桁が大きい場合、桁上げを先に計算すると桁上げ伝播より演算時間は短いのか?
CLAの桁上げの計算は、すべての桁に対して、与えられた入力から
一斉に始められますから、すべての桁の桁上げが求まるまでの時間は
一般にCLAのほうが速くなります。
20入力などの入力の多いICは作れないのか?
理論上はつくれますが、速度が遅くなるため、あまり現実的ではありません。
またCMOS回路の場合は、基板バイアス効果があるので、
すべてのnMOS・pMOSのB(基板)の電位を独立に設定できなければ、
あまり段数が多すぎると正しく動作しなくなります。
論理回路では回路規模が大きくなると電圧が下がって出力の論理値が反転してしまうことはないのか?
CMOS回路の場合は、出力は常にVDDかGNDのどちらかに直流的につながりますので、
VDDかGNDにいたる経路のMOSトランジスタのON抵抗の総和による電圧降下が
問題になるほど電流を流さない限りは、そいうことは起こりませんね。
除算が減算の繰り返しとどういうことか?
例えば12÷3=4、というのは、12-3-3-3-3=0、つまり、3を4回引いたらゼロになる、
という意味の計算です。
EXORの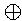 の読み方を教えてください。
の読み方を教えてください。
さて、なんと読むのでしょう・・・
ブール代数は代数形の構造が良い反面、and,or回路よりもnand,nor回路のほうが回路の段数が少なくなることからもわかるように、式の簡単さと回路の高速さの対応が完全でないという欠点があると思います。ブール代数とは別に回路の簡単さに対応した演算を基にした代数を考えることに意味はあると思います。このような体系化された代数系はありますか?また、新しく代数系を考えるのとは別の方法で、ある論理表に対応する最適な回路を知る方法はありますか?
ご指摘のように、CMOS回路の場合は、nand,norを使うほうが得策です。
それは、ブール代数の範囲内で扱うことができると思います。
つまりnot,and,orを基本演算子とするのではなく、
not,nand,norを基本演算子として、式変形をする、という意味です。
このような扱い方で、論理回路を扱うのが一般的のように理解しています。
また、後半の話は、一般に論理回路の最適化はNP困難な問題なので、任意の論理式に対して最適な回路を求める方法は知られていません。
加算器の高速化は未だに研究されているとのことですが、たまに間違える代わりに非常に高速な加算器には価値はあると思いますか?もちろん、間違えたことの判定も十分に高速にできると考えることにします。
非常に面白い考え方だと思います。
演算精度は、場合によっては全桁分は必要ない、という考え方もできると思います。
個人的には非常に興味がある考え方です。
また間違い(とその検出)を仮定する演算システム、という考え方も、
2つの考え方があって、上述のものは、ある程度の間違いは許す、ということでしょうし、もう一つは、勢いだけで動くけど、ちゃんとスーパーバイザ(監視)をつける、という考え方、でしょうね。
後者も、実現方法はすぐには思いつきませんが、従来にはなさそうな考え方で、非常に面白いと思います。
戻る
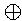 の読み方を教えてください。
の読み方を教えてください。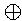 の読み方を教えてください。
の読み方を教えてください。