第7回: 演算器の高速化

今回は、ちょっとVHDLから離れて、加算器と乗算器の高速化の手法についてみていくことにしましょう。

加算器の高速化

全加算器と生成項・伝播項

コンピュータは演算を行うもの、で、すべての演算は加算から導かれますから、加算を行う加算器 (adder)は、まさにコンピュータの基本要素といえます。そして2進数で数値・データをあらわす現在のコンピュータでは、 2進数の加算を行う加算器が必要なわけですが、結局1桁分の2進数の加算を行う「1ビット加算器」があれば、それを組み合わせて何桁の加算、さらにはどんな演算もできますから、 1ビットの加算器こそ、コンピュータの究極の基本要素といえます。

加算対象の2つの1ビットの数An, Bnと、前の桁からの桁上げ信号Cn-1を加算し、その結果Snと、次の桁への桁上げ信号Cnを生成するのが、1ビットの加算器である 全加算器 (full adder; FA)でした。この全加算器の出力であるSn, Cnのうち、Snは

Sn = AnBnCn-1

とかけますが、桁上がりについて、もう少し考えてみると、桁上がりが発生する(Cn=1となる)場合は、次のいずれかです。

An+Bnで桁上がりが発生するとき(このとき、Cn-1には無関係に発生する)：「生成」
AnとBnの片方が1で、さらにCn-1が1のとき：「伝播」

この2つを分けて考えると、次のような論理式を書くことができます。

Gn = An・Bn (生成項)
Pn = An Bn (伝播項)
Cn = Gn + Pn・Cn-1 (生成項=1または「伝播項=1かつCn-1=1」のとき、Cn=1)

ところがQn=An + Bnとおくと、 PnとQnの違いはAn=Bn=1のときだけで、Pn=0, Qn=1となりますが、このときは生成項Gn=1なので、伝播項Qnに関係なく無条件にCn=1となります。言い換えると、Cnは次のように書いても、結果はまったく同じであるわけです。

Cn = Gn + Qn・Cn-1

これらの式を使って、全加算器をつくることができるわけです。

リプルキャリー加算器

N桁の(2進数の)加算を行う最も簡単な構成は、N個の全加算器をつなぐもので、リプルキャリー加算器桁上げ伝播加算器(Ripple Carry Adder; RCA)と呼ばれます。つまり次の図のように、N個の全加算器をつなぐわけです。

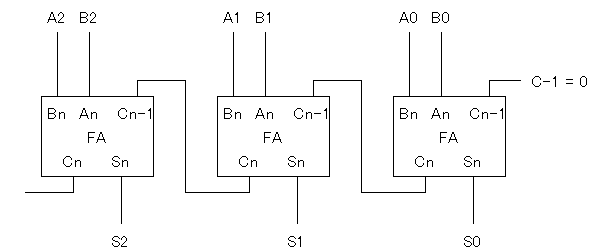リプルキャリー加算器では、前の桁の桁上げ(キャリー)が次の桁の入力につながっていますので、最大ですべての桁、つまり桁数分(=N)のキャリーの伝播が起こることになり、全体として加算が終了するまでの時間(演算時間)は桁数Nに比例する、という問題点があります。

桁上げ先見加算器

さきほどの全加算器の論理式は、キャリーが生成する場合(生成項)と伝播する場合(伝播項)に分けて、次のように書くことができました。

Gn = An・Bn (生成項)
Pn = An Bn (伝播項)
Cn = Gn + Qn・Cn-1 (生成項=1または「伝播項=1かつCn-1=1」のとき、Cn=1)

(または Qn = An + Bn とおいて、Cn = Gn + Qn・Cn-1)

たとえば4ビット加算器をつくるとして、この生成項と伝播項を順番に書くと次のようになります。

G0 = A0・B0 P0 = A0B0 C0 = G0 + P0・C-1

G1 = A1・B1 P1 = A1B1 C1 = G1 + P1・C0

G2 = A2・B2 P2 = A2B2 C2 = G2 + P2・C1

G3 = A3・B3 P3 = A3B3 C3 = G3 + P3・C2

このうち、C1は次のように書くことができます。
C1 = G1 + P1・C0 = G1 + P1・(G0 + P0・C-1) = A1・B1 + (A1B1){A0・B0 + (A0B0)・C-1}
つまり、C1が、前の桁からの桁上がりC0を使わずに、入力An, Bn(とC-1)のみであらわせることになります。同様に、C2, C3も、入力An, Bnのみであらわすことができます。

C2 = G2 + P2・C1 = G2 + P2・(G1 + P1・C0) = G2 + P2・(G1 + P1・(G0 + P0・C-1)) = G2 + P2・G1 + P2・P1・G0 + P2・P1・P0・C-1
C3 = G3 + P3・(G2 + P2・(G1 + P1・(G0 + P0・C-1))) = G3 + P3・G2 + P3・P2・G1 + P3・P2・P1・G0 + P3・P2・P1・P0・C-1

ちなみにSn = Pn + Cn-1ですから、これらを使うと、この4ビット加算器の回路図は次のようになります。

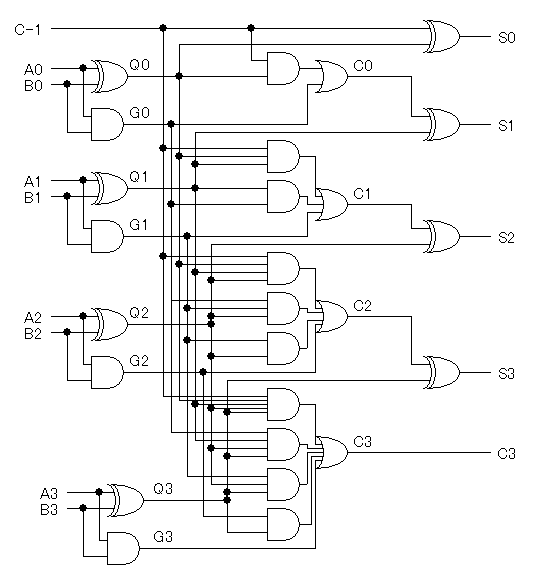
この構成では、RCAのようなキャリーの伝播は起こらず、すべての桁のキャリーが、入力An, Bnのみから決まるため、 RCAのように桁数に比例した演算時間がかかることはありません。このような構成の加算器を キャリー先見加算器 (Carry Look-ahead Adder; CLA) と呼びます。 (※上図中のQ0～Q3はそれぞれP0～P3の間違いです)

このようにCLAは桁数が多くても高速な演算が可能ですが、桁数が多くなるほど、キャリーCnを求めるための論理式が急激に複雑になり、論理回路が大規模になってしまうという問題があります。 (元気がある人は8ビットCLAでも作ってみましょう・・・) 現実的にはCLAの構成は4ビット分にとどめ、それ以上のビット数の加算器が必要な場合は、4ビットCLAをつなげる、という構成をとるのが一般的です。

乗算器の高速化

乗算は加算の繰り返しですが、非常によく使う演算なので、乗算を行う乗算器自体に関しても、いろいろな工夫が知られています。

2進数の乗算

乗算の基本は、やはり筆算です。例えば4桁の2進数の掛け算「1001×0101」(10進数で、9×5=45)を次のように求めることができるでしょう。

    1001  ：被乗数(X)
×) 0101  ：乗数  (Y)
----------
    1001  ：部分積
   0000
  1001
 0000
---------
 0101101 (0x2d = 45(dec))

乗数Yの各桁に対して、被乗数Xを順番にずらして並べていき、最後にすべてを足すわけですが、途中の、被乗数Xを順番にずらしていった項を 部分積と呼びます。部分積を求めるのは簡単で、被乗数Yの、その桁が1であればXそのもの、その桁が0であれば0、となります。

並列乗算器

もっとも直感的な乗算器の作り方は、この筆算をそのまま回路にする、というものです。つまり部分積x_i・y_jを求める回路と、上から下へ部分積を加算していく、という筆算の手順のとおりに並べる、という方法です。

[p.75]の図は、このような方法による8ビットの乗算器(並列乗算器)の例です。結局1桁の2進数の乗算は、AND演算そのものですから、それぞれの部分積x_i・y_jをANDゲートで求めつつ、上から下へ足していく加算を行う回路を並べていけばよいことになります。このような構成の乗算器を並列乗算回路と呼びます。

並列乗算回路では、部分積の段数、つまり乗数Yの桁数分とほぼ等しい数だけ加算器が並びますので、この段数が、全体の演算時間を決めるもっとも大きな要因となります。

ブースのアルゴリズム

乗算器の高速化のためには、部分積の段数を減らすことが効果的ですが、そのためのうまい方法として、ブースのアルゴリズム (Booth's algorithm) というものが知られています。

詳細は省略しますが、乗数Yに対して、次のようなYjYjを求めると、 Yのビット数の半分の数のYjを加算するだけで乗算結果を求めることができる、というものです。（ただしy_jは、乗数Yのjビット目）

Yj = y_2j +y_2j-1 - 2y_2j+1

つまり、部分積の加算数を半分にできるため、その分、高速化をすることができることになります。

配布資料

戻る

G0 = A0・B0	P0 = A0B0	C0 = G0 + P0・C-1
G1 = A1・B1	P1 = A1B1	C1 = G1 + P1・C0
G2 = A2・B2	P2 = A2B2	C2 = G2 + P2・C1
G3 = A3・B3	P3 = A3B3	C3 = G3 + P3・C2