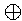 Bn
Bn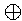 Cn-1
Cn-1
library ieee;
use ieee.std_logic_1164.all;
use ieee.std_logic_arith.all;
use ieee.std_logic_unsigned.all;
entity alu is
port (
a, b: in std_logic_vector(7 downto 0);
opcode: in std_logic_vector(2 downto 0);
x: out std_logic_vector(7 downto 0)
);
end alu;
architecture arch of alu is
begin
process (a, b, opcode)
case opcode is
when I_AND => x <= a and b;
when I_OR => x <= a or b;
when I_NOT => x <= not a;
when I_XOR => x <= a xor b;
when I_ADD => x <= a + b;
when I_SUB => x <= a - b;
when I_ACC => x <= a;
when I_DAT => x <= b;
when others => x <= "XXXXXXXX";
end case;
end process;
end arch;
package alu_pack is
constant I_AND: std_logic_vector(2 downto 0) := "000";
...
end alu_pack;
このALUのVHDL記述そのものは、意外と単純で、行う演算を指定する
opcodeの値に応じて、出力xを、入力a, bから求める式を
case文で切り替えているだけ、です。
(ちにみに後半のpackage以下で、演算の指定に使っている
I_ANDなどの定数の値を定義しています。C言語での#defineのようなものと
理解しておいてください)
ここでちょっと面白いのは、その論理合成結果[p.77「論理回路図」]です。 1ビット分のALUは、入力であるa[n], b[n]からいろいろな演算回路を通し、、 そのうちの1つをopcaodeによって、セレクタを使って選ぶ、という 構成になっています。(※セレクタは[p.67]参照) 上から4つの論理演算は、そのまんま、なのですが、 真ん中の加算・減算のところが、ちょっと一工夫があります。 opcode=100のときは、xはa+b(加算)なので、加算器を通した 結果がxに出てきますが、この加算器のcin(下の桁からの桁上げ)は、 下半分の図からわかるように、最下位ビットのALUでは、opcode[0]に なっています。 opcode=100(加算)のときは、opcode[0]=0ですので、 まさに桁上げ伝播加算器(RCA)の構成となります。
ところがoppcode=101(減算)のときは、加算器のb側には b[n]をNOTゲートを通したもの(/b)が与えられています。 またこのときopcode[0]=1ですので、全体としては、 「a + /b + 1」が求められることになります。 ところが、/b + 1 とは、bの「2の補数」ですので、 2進数の数としては、bの符号を反転したもの(-b)と同じ意味となります。 (2の補数については、ここなどを参照) つまり出力xは、「a - b」と同じ意味となり、減算が行われていることに なります。
加算対象の2つの1ビットの数An, Bnと、前の桁からの 桁上げ信号Cn-1を加算し、その結果Snと、次の桁への 桁上げ信号Cnを生成するのが、1ビットの加算器である 全加算器 (full adder; FA)でした。 この全加算器の出力であるSn, Cnのうち、Snは
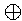 Bn
Bn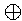 Cn-1
Cn-1
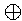 Bn (伝播項)
Bn (伝播項)
 リプルキャリー加算器では、前の桁の桁上げ(キャリー)が
次の桁の入力につながっていますので、最大ですべての桁、つまり
桁数分(=N)のキャリーの伝播が起こることになり、
全体として加算が終了するまでの時間(演算時間)は
桁数Nに比例する、という問題点があります。
リプルキャリー加算器では、前の桁の桁上げ(キャリー)が
次の桁の入力につながっていますので、最大ですべての桁、つまり
桁数分(=N)のキャリーの伝播が起こることになり、
全体として加算が終了するまでの時間(演算時間)は
桁数Nに比例する、という問題点があります。
 Bn (伝播項)
Bn (伝播項)
たとえば4ビット加算器をつくるとして、 この生成項と伝播項を順番に書くと次のようになります。
| G0 = A0・B0 | P0 = A0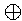 B0 B0 |
C0 = G0 + P0・C-1 |
| G1 = A1・B1 | P1 = A1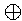 B1 B1 |
C1 = G1 + P1・C0 |
| G2 = A2・B2 | P2 = A2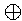 B2 B2 |
C2 = G2 + P2・C1 |
| G3 = A3・B3 | P3 = A3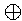 B3 B3 |
C3 = G3 + P3・C2 |
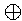 B1){A0・B0 + (A0
B1){A0・B0 + (A0 B0)・C-1}
B0)・C-1}
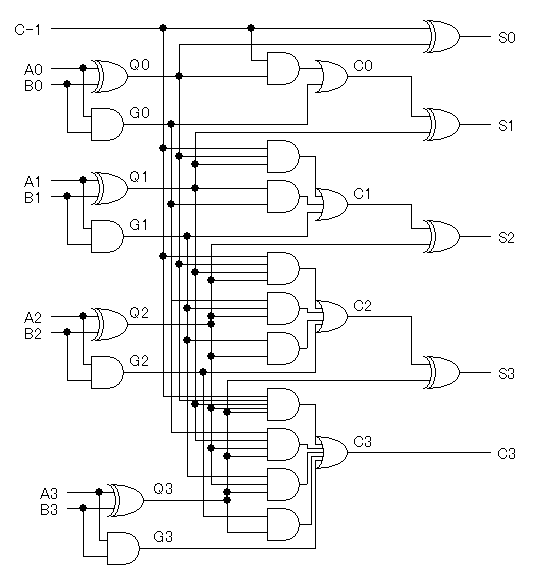
このようにCLAは桁数が多くても高速な演算が可能ですが、 桁数が多くなるほど、キャリーCnを求めるための論理式が 急激に複雑になり、論理回路が大規模になってしまうという問題があります。 (元気がある人は8ビットCLAでも作ってみましょう・・・) 現実的にはCLAの構成は4ビット分にとどめ、それ以上のビット数の 加算器が必要な場合は、4ビットCLAをつなげる、という構成をとるのが 一般的です。
1001 :被乗数(X)
×) 0101 :乗数 (Y)
----------
1001 :部分積
0000
1001
0000
---------
0101101 (0x2d = 45(dec))
乗数Yの各桁に対して、被乗数Xを順番にずらして
並べていき、最後にすべてを足すわけですが、
途中の、被乗数Xを順番にずらしていった項を
部分積と呼びます。
部分積を求めるのは簡単で、
被乗数Yの、その桁が1であればXそのもの、
その桁が0であれば0、となります。
[p.75]の図は、このような方法による8ビットの乗算器(並列乗算器)の 例です。 結局1桁の2進数の乗算は、AND演算そのものですから、 それぞれの部分積xi・yjをANDゲートで求めつつ、 上から下へ足していく加算を行う回路を並べていけばよいことになります。 このような構成の乗算器を並列乗算回路と呼びます。
並列乗算回路では、部分積の段数、つまり乗数Yの桁数分と ほぼ等しい数だけ加算器が並びますので、 この段数が、全体の演算時間を決めるもっとも大きな要因となります。
詳細は省略しますが、乗数Yに対して、次のようなYjを求めると、 Yのビット数の半分の数のYjを加算するだけで 乗算結果を求めることができる、というものです。 (ただしyjは、乗数Yのjビット目)