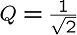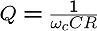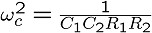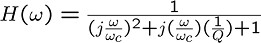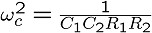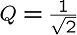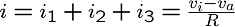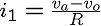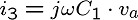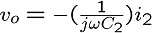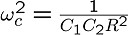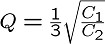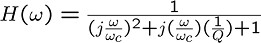第4回: オペアンプ(その2)の演習

LC 2次フィルタ (復習)

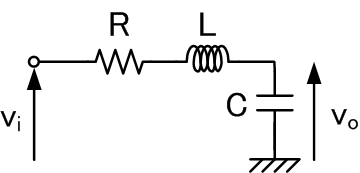
この図のようにLとCとRからなる回路の入力v_iと出力v_oの比、すなわち伝達関数H(ω)を求めみると、次のようになります。

ここで、

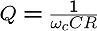
です。 2次のローパスフィルタ(LPF)は、一般にこのような形の伝達関数をもつわけです。このω_Cは、伝達関数の特性が通過域から遮断域に変わる境目の周波数であるため、カットオフ周波数と呼ばれます。

オペアンプを使ったフィルタ(VCVS型LPF)の伝達関数

前回のVCVS型LPFの伝達関数は、このような式でした。

ここで、

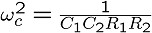
とおいてみると、次のように書くことができます。

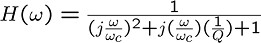
これから、このVCVS型LPFは、確かに2次のLPFであることがわかります。

VCVS型LPFの設計

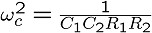
[演習]

このVCVS型LPFで、

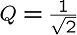
となるように、 C₁, C₂, R₁, R₂の値を求め、設計した回路図を描いてみてください。ただしR₁=R₂=1kΩとします。
解: C₁=1.4μF, C₂=0.7μF, 図略

VCVS型LPFのシミュレーション

ためしに、このVCVS型LPFのシミュレーションをやってみましょう。

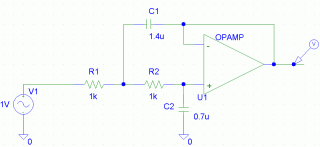
↑回路図を入力します。今回は、出力電圧が、入力信号の周波数によってどのように変わるか、を観測したいわけですが、これは、いわゆるAC解析になります。そこで、入力電圧源(V1)に、AC解析用の電源(VAC)を使うようにします。

↑V1のパラメータはいろいろありますが、とりあえずは振幅(ACMAG)を1Vに設定してみます。

↑シミュレーションを行う対象を、 Analysis→Setupから設定します。具体的には、AC解析(AC Sweep)のEnabledにチェックをいれ、さらに細かい条件を設定するために AC Sweepのボタンを押します。

↑周波数特性は、ふつうは周波数を10のべき乗で変化させるので、AC Sweep Typeを"Decade"(10倍)にし、開始(Start Freq.)と終了(End Freq.)の周波数を、とりあえず10(=10Hz)を1MEG(=1MHz)にしておきます。

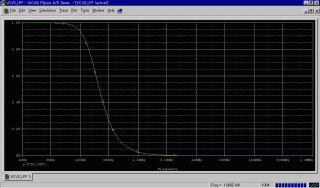
↑シミュレーションを実行すると、出力電圧が入力信号の周波数とともにどのように変化するか、の結果が得られます。 (ちなみに今回は入力電圧の振幅は1Vにしてありますから、この出力電圧の値そのものが、伝達関数H(ω)の絶対値、ということになります。)

一応これでシミュレーションはできたのですが、このような伝達関数は、縦軸を対数軸にして描くのが一般的です。そこで、縦軸の設定を変更してみましょう。

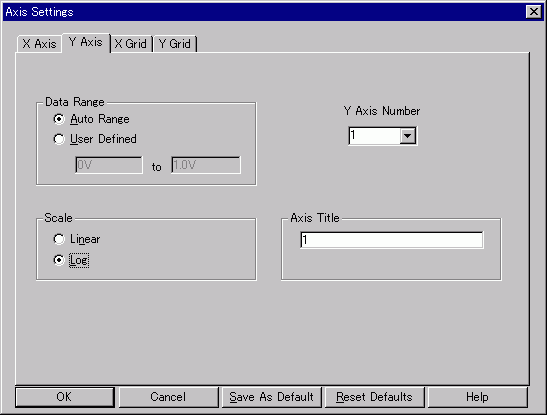
↑Plot→Axis Settingsで、軸の設定ができます。その中の縦軸(Y軸)の設定をするために、 "Y Axis"のタブの中の"Scale"を、"Log"にしておきます。

↑すると、縦軸が対数軸になってグラフが描かれます。確かにLPFの特性になっていることがわかります。

ちなみに、カットオフ周波数が設計したとおりの値になっているかを確認しておきましょう。カットオフ周波数では、伝達関数の絶対値は 1/√2(=約0.71)となります。今回設計したLPFのカットオフ周波数は、 ω_C=1kHzでしたから、これを周波数f_Cで表すと、 f_C=ω_C/2π=159Hzとなります。

このグラフ上の点の座標を読むために、 Trace→Cursor→Displayでカーソルを表示させ、 159Hz付近をクリックしてみると、それに対応するYの値(=出力の電圧)がわかります。

↑確かに、f=159Hz程度で715mV程度となっていることがわかります。

オペアンプを使ったフィルタ(その2: 多重帰還型)

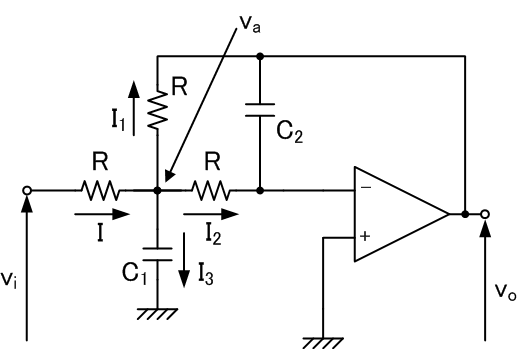
オペアンプを使った、別の能動フィルタを紹介しておきましょう。この図のような回路を考えてみます。これも地道に回路方程式をたてていくことにしましょう。

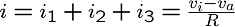
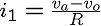
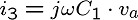
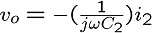
これからi₁～i₃を消去し、続いてv_aを消去すると、次のような関係式が得られます。

ここで、

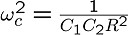
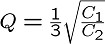
とおくと、やはり次のように2次LPFの伝達関数の式になることがわかります。

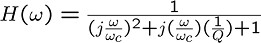
※この最後の式は、マイナスがつくのが正しいです(2015/7/30追記)

課題2

定められたカットオフ周波数をもつVCVS型LPFを作成し、その動作をシミュレーションで検証してください。ただしカットオフ周波数f_Cは、「自分の名列番号+1」[kHz]とすること。 (例えば名列番号1の人は、カットオフ周波数f_C=2kHzの VCVS型LPFを作成する) なお、たとえばR1=R2=1kΩなどを仮定してよい。 ※角周波数ω_Cではないので注意

提出物:
- 設計した回路の*.schファイル
- シミュレーション結果(画面をキャプチャしたビットマップファイルや、図として貼り付けたWordファイル等)
- メール本文には、名前とfc, R1, R2, C1, C2の値を記載する
提出方法:
- 上記内容の本文のメールに上記2点を添付し、秋田まで送付 (2つのファイルをzip等で圧縮するのが望ましい)
- メールの題名(Subject)は、"ic2_2-??" (ただし??の部分は自分の名列番号)とすること
締切: 11/7(金) 10:30
注意: 友達と相談したり、文献・Webページ等を参考にすることは大いにやってください。ただし、参考にしたものを、必ず「出典」として明記すること。(無断借用(パクり)は厳禁です) 友達に教える場合も、結果だけ渡すのではなく、過程を含めて教えてあげてください。

この回のソボクな疑問集

戻る