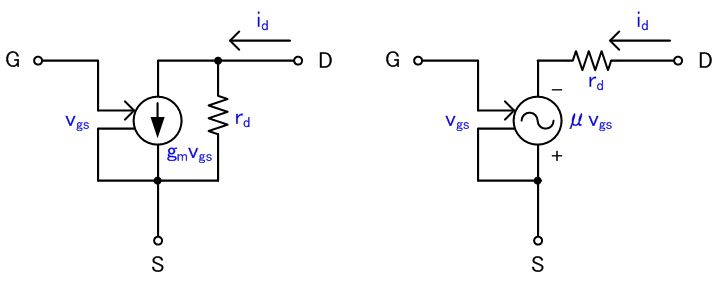
このグラフを、MOSトランジスタの静特性と呼びます。
今日は、オペアンプの中にも使われている、電子回路の基本素子であるMOSトランジスタについて見ていくことにしましょう。
シリコンなどの半導体には、電子が多いN型と、ホール(電子が抜けた穴)が多いP型の2種類がありますが、これを次のように組み合わせた素子を考えてみましょう。

この素子は、上から順に金属(Metal)、絶縁膜(酸化物; Oxide)、半導体(Semiconductor)が積み重なった構造になっているので、
それぞれの頭文字をとってMOSトランジスタと呼びます。
そして、真ん中の電極をゲート(G)、その両側のN型の領域についている電極を、それぞれソース(S)、ドレイン(D)と呼びます。
MOSトランジスタの動作を、それぞれの電極に与える電圧と、流れる電流の関係で考えてみることにしましょう。
電極が3つありますので、ソース(S)を基準としたゲート(G)の電圧VGS と、ソース(S)を基準としたドレイン(D)の電圧VDS 、 さらにドレイン(D)を流れる電流ID を考えることにしましょう。
VGS が負のときは、ゲート(G)の真下の領域はP型半導体の中のホールが引き寄せられてくるため、P型のまま、
つまりソース(S)-ドレイン(D)間に電流は流れません。
つまり I D = 0 となります。
今度はVGS を正にしてみましょう。ただしあまりVGSが大きくないとします。
このときには、ゲート(G)の真下の領域には、P型半導体中に少しだけ存在する、電荷が負の電子が集まってきます。
つまりゲート(G)の真下の領域が、電子が多い領域になりかけている、わけです。
ただしまだ電子が多少多いだけで、ソース(S)-ドレイン(D)間には、やはり電流は流れません。
つまり I D = 0 となります。
VGSを正でさらに大きくしてみましょう。
ある程度大きくなると、ゲート(G)の真下の領域の電子の濃度が高くなり、実質的にN型になります。
つまりソース(S)-ドレイン(D)間は、N型半導体でつながるわけで、電流が流れることになります。
この状態で、ゲート(G)の真下にできているN型の領域をチャネル (channel)と呼びます。
この状態では、VGS を増やすほど、I D も大きくなることになります。
このようにチャネルが形成されるのに必要なVGS のことをしきい値電圧 (threshold voltage)と呼び、
VT と書くことにしましょう。
以上から、MOSトランジスタに流れる電流 I D は、VGS によって制御することができることになります。
VGS > VT 、つまりチャネルが形成されている状態で、VDS を変えてI D を見てみることにしましょう。
このときは、チャネルは形成されていますが、I D を流すための電圧がないわけですから、I D = 0 となります。
VDS > 0ならば、VDS を増やすほど I D は増えていくはずです。
この状態を非飽和領域と呼びます。
非飽和領域では、VDS を増やすほど I D は増えていくわけですが、
ドレイン(D)の端のところのP型領域(チャネルができている)で実質的に加わっている電圧は VGS - VDS ですから、
これがしきい値電圧 VT よりも小さくなってしまうと、チャネルが形成されなくなってしまいます。
VGS - VDS > VT つまり VDS < VGS - VT
であるわけで、逆に言うと、VDS をVGS - VT よりも大きくしてしまうと、
ドレイン(D)の端のところでチャネルができないことになります。
この現象をピンチオフと呼びますが、もちろんチャネルが部分的に形成されなくても、
途中までチャネルを流れてきた電子は、このピンチオフしている点からドレイン(D)領域まで一気に加速されていきますので、
電流 I D 自体は流れます。
ただし VDS を増やしても、ピンチオフしている点が移動してチャネルが短くなっていくだけで、
I D はほとんど変わらなくなってしまいます。
この状態を飽和領域と呼びます。
以上から、I D と VDS の関係は次のようなグラフとなるでしょう。

このグラフを、MOSトランジスタの静特性と呼びます。
ちなみにMOSトランジスタは、下の図のような記号で描きます。
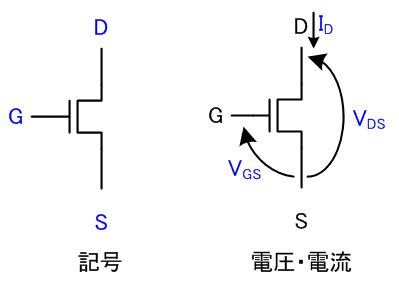
MOSトランジスタを使った回路を考えるときには、主にこの静特性のグラフを使うことになりますが、
通常は、ある電圧(VGS 、VDS )を中心として、少しだけ上下に電圧を、扱いたい信号にあわせて「振る」ということをやります。
このような中心点を動作点と呼び、このバイアス点を中心に小さく振る、扱いたい信号を小信号と呼びます。
例えば先のMOSトランジスタの静特性のグラフで、
(VGS 、VDS ) = (3V, 6V) を中心にVGS を±0.5V、つまり VGS = 2.5V 〜 3.5Vに振ると、
I D がそれに応じて変わる、というように使います。
このような使い方をするとき、MOSトランジスタの、「振られている」信号に対する等価回路、を考えると、
MOSトランジスタを含む回路を考えやすくなることがあります。
このような、振られている小さい電圧の変化(小信号)に対するMOSトランジスタの等価回路を考えてみましょう。
MOSトランジスタの I D は、VGS と VDS によって、
静特性のグラフのように変わりますから、次のような式で書くことができるでしょう。
![]()
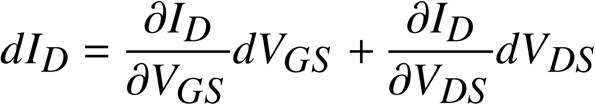
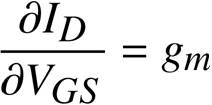
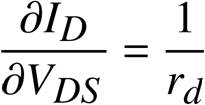
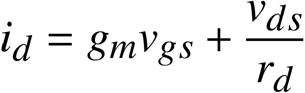
もちろんMOSトランジスタのゲート(G)は、ドレイン(D)やソース(S)、チャネルから電気的に離れていますから、ゲート(G)には電流が流れません。
そこで、この動作点付近の変化 vgs などに対しては、次のようなMOSトランジスタの等価回路(小信号等価回路)を考えることができるでしょう。