 xN-1) }
xN-1) }
 QN
QN
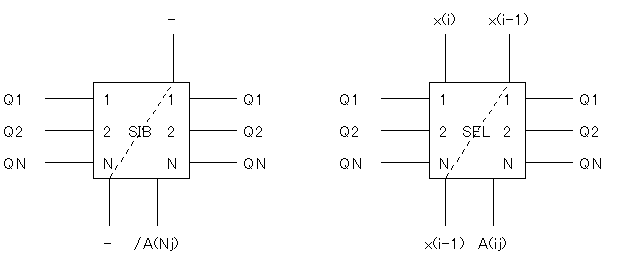
まずANjは符号ですから、QN=0のときにはZjの符号はXの符号と同じであり、 逆にQN=1のときにはYjが負となるためにXの符号を反転させる必要があります。
同様に、Q1=1のときにはXを2jビットシフトさせるのですが、 このZjの式には、2jビットシフトさせる22jがすでにありますから、 j桁目、つまりAijは、Xのj桁目xjと同じになります。 しかしQ2=1のときには、Xを(2j+1)ビットシフトさせる必要があるので、 結果としてj桁目のAijは、Xの(j-1)桁目xj-1と同じになります。
さらにQN=1のとには、Aijを求めるのに 2の補数をとらなければなりませんから、Aijを反転させ(1の補数)、 全体に1を加える必要があります。
以上から、Q1, Q2, QNとANj, Aij, Cjは 次のような関係になるでしょう。
| Q1 | Q2 | QN | ANj | Aij | Cj |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | xN-1 | xi | 0 |
| 0 | 1 | 0 | xN-1 | xi-1 | 0 |
| 0 | 1 | 1 | /xN-1 | /xi-1 | 1 |
| 1 | 0 | 1 | /xN-1 | /xi | 1 |
 xN-1) }
xN-1) }
 QN
QN
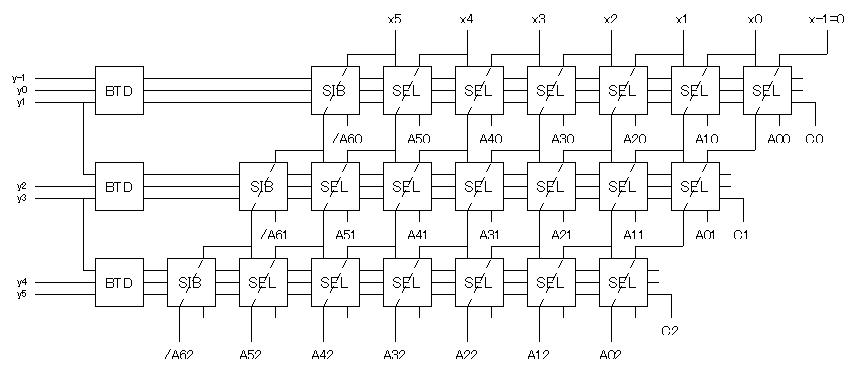
| Z | = | Σj=02(-1・A6j・26 + Σi=05Aij2i + Cj)22j |
| = | Σj=02{ Σj=05Aij2i + Cj}・22j - { A6224 + A6122 + A6020}・26 | |
| = | Σj=02{ Σj=05Aij2i + Cj}・22j + { /A6224 + 1・23 + /A6122 + 1・21 + /A6020 + 1・20 } ・26 | |
| (※2の補数をとるために、各ケタごとに反転していることに注意) | ||
| = | Σj=02{ A5j25 + A4j24 + A3j23 + A2j22 + A1j21 + A0j20 + Cj}・22j + Σj=02{ /A6j22j・26 } + 25・22・2 + (25 + 24) 22・1 |
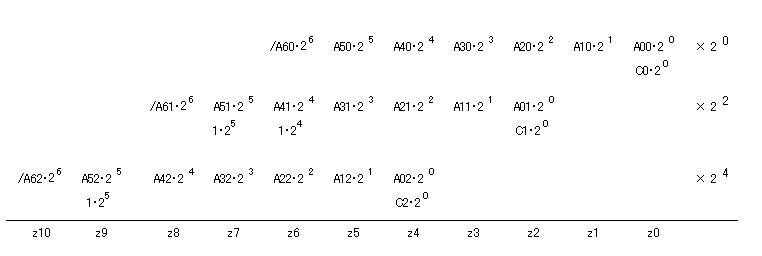
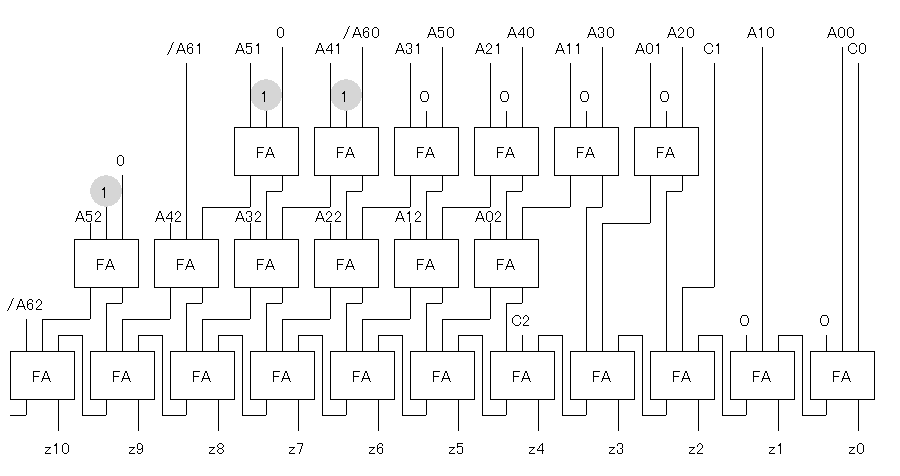
この「和」を求める操作を、何ビットかをまとめて行ってしまうと、
結果として部分積を求める全加算器の段数を減らすことができます。
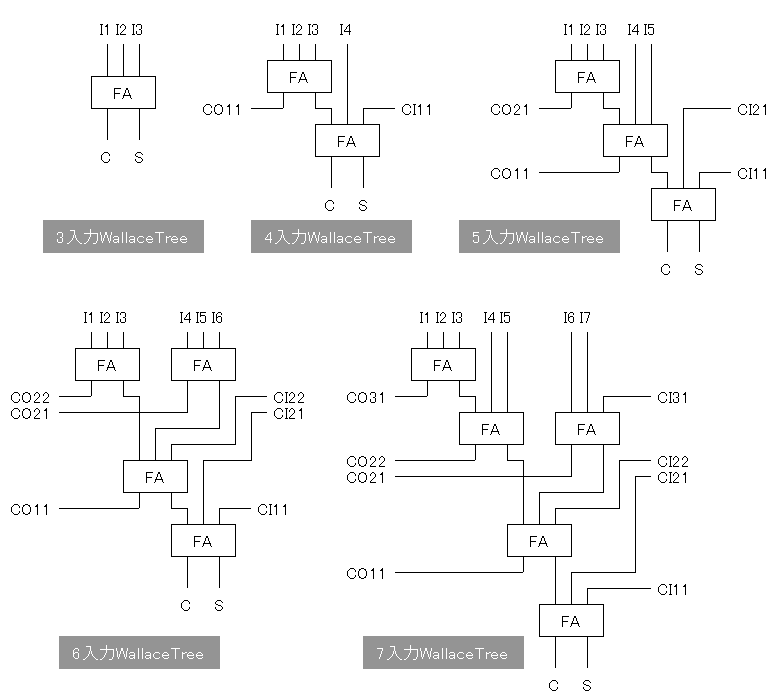
何ビット分をまとめるかによって構成は変わってきますが、
3〜9ビット分について、まとめてみました。
このような回路をワレスの木 (Wallace Tree)と呼びます。
(ビット数が4以上の場合には、加算の結果が{C, S}の2ビットを超えるので、
キャリー入力CIとキャリー出力COがあることに注意)
何ビット分まとめるか、は、回路規模や演算速度などから
選択することになります。
このワレスの木を部分積の和のところに使った回路を
例として「眺めて」おくことにしましょう。
例えば四角で囲ったところに、(6入力の)ワレスの木が
使われていることがわかります。

(出典: 榎本忠義「CMOS集積回路」p.169より抜粋)
※クリックすると大きくなります
| 乗算器A | 乗算器B | 乗算器C | |
| 構成(部分積生成) | 2次ブース | 2次ブース | 2次ブース |
| 構成(部分積加算) | CSA | Wallace木 | Wallace木 |
| 構成(桁上げ吸収) | BCLA | BCLA | CLA |
| 最高動作周波数[MHz] | 134.6 | 156.3 | 83.2 |
| MOSFET数(部分積生成)[個] | 3,328 | 3,328 | 3,328 |
| MOSFET数(部分積加算)[個] | 3,780 | 3,136 | 3,136 |
| MOSFET数(桁上げ吸収)[個] | 1,990 | 1,990 | 1,376 |
| MOSFET数(全体)[個] | 9,098 | 8,454 | 7,840 |