第5回: 加算器(その3)
全加算器の回路
今回はまず、すべての演算の基本要素である全加算器そのものの
構成方法をいくつか見ていくことにしましょう。
CMOS論理回路での全加算器 (その1)
まず一番素直な作り方は、全加算器の真理値表から
論理回路を作る方法です。
An Bn Cn-1 | Cn Sn
-----------+------
0 0 0 | 0 0
0 0 1 | 0 1
0 1 0 | 0 1
0 1 1 | 1 0
1 0 0 | 0 1
1 0 1 | 1 0
1 1 0 | 1 0
1 1 1 | 1 1
この全加算器の真理値表から、積和標準形で論理式を求めると
次のようになるでしょう。(一部、カルノー図を使った簡略化をしています)
- Sn = An・Bn・Cn-1 + An・/Bn・/Cn-1 + /An・/Bn・Cn-1 + /An・Bn・/Cn-1
- Cn = An・Bn + An・Cn-1 + Bn・Cn-1 = An・Bn + Cn-1・(An + Bn)
これから論理回路を作ると、けっこう大きな論理回路になるでしょう。
(回路図は省略: インバータ3個、ANDゲート7個、ORゲート2個のはず)
CMOS論理回路での全加算器 (その2)
上の作り方から、少し工夫をしてみましょう。
というのも、桁上げ伝播加算器(RCA)での例からもわかるように、
加算器では、とにかくキャリーが出てくるまでの時間がネックになることが
多々あります。
(いわゆるクリティカルパス (critical path))
そこで少しでもキャリーを先に求めよう、という方針で、
次のように式を書き換えてみます。
- Cn = An・Bn + Cn-1・(An + Bn)
- Sn = An・Bn・Cn-1 + (An + Bn + Cn-1)・/Cn
つまりCnを求める式は同じですが、
その結果を使って、Snを求めているわけです。
具体的には、Sn=1となるのが、、次の2通りのいずれか、というわけです。
- An = Bn = Cn-1 = 1の場合
- Cn = 0(つまりAn, Bn, Cn-1のうち、1が1個以下)の場合で、
An, Bn, Cn-1のどれか1個が1の場合(An=1, Bn=Cn-1=0 など)
ポイントは、先にCnを求めて、それを外に出しつつ、
あまり急がない(クリティカルパスになりにくい)Snは、
その結果を使ってゆっくり求めよう、という方針です。
次のような回路になるでしょうか。
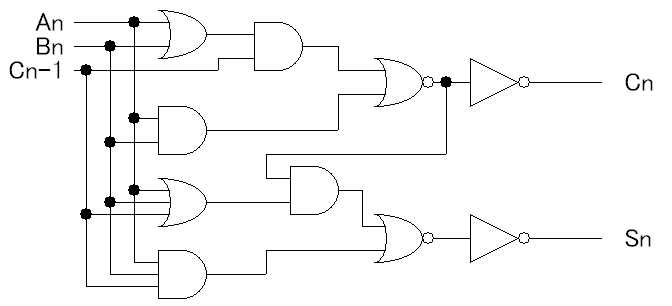
トランスファゲートを使った全加算器
トランスファゲートをうまく使うと、さらに少ないトランジスタ数で
全加算器をつくることができます。
まずは排他的論理和(EXOR)ゲートを紹介しておきましょう。
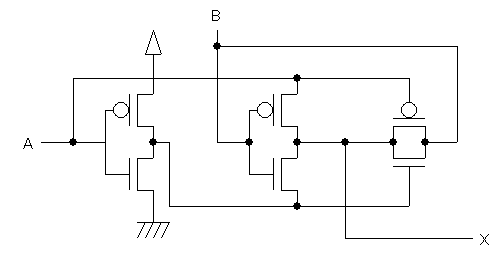
A, Bが1のときはA, Bは電源電圧(高い電圧)になり、
A, Bが0のときはA, Bは0Vになる、ということに注意すると、
たしかにEXORゲートになっていることがわかります。
(なかなかうまいことを思いつく人がいるものです)
ちなみにトランスファゲートを使うと、
Aの値によって、X, Yのいずれかが出力Zに出てくる、
次のようなセレクタも作ることができるのでした。
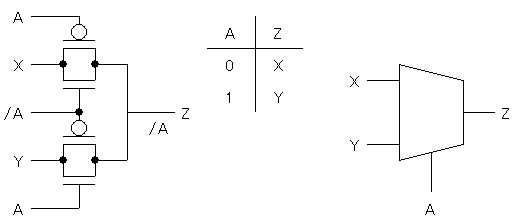
これを使うと、次のように全加算器をつくることができます。
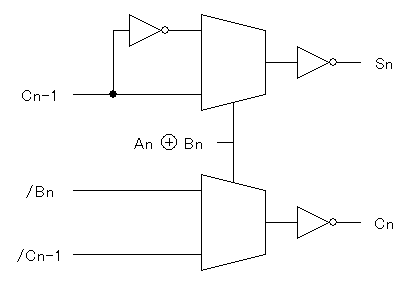
これは、まずSnは次のように求められることから導かれています。
- An = Bn (つまりAn
 Bn=0)のときは、Sn = Cn-1
Bn=0)のときは、Sn = Cn-1
- An != Bn (つまりAn
 Bn=1)のときは、Sn = /Cn-1
Bn=1)のときは、Sn = /Cn-1
またCnは次のように求められることから導かれています。
- An = Bn (つまりAn
 Bn=0)のときは、
An=Bn=1ならばCn=1、An=Bn=0ならばCn=0、つまりCn=Bn ( =An)
Bn=0)のときは、
An=Bn=1ならばCn=1、An=Bn=0ならばCn=0、つまりCn=Bn ( =An)
- An != Bn (つまりAn
 Bn=1)のときは、
An, Bnのどちらか一方は1なので、Cn-1=1ならばCn=1、つまりCn = Cn-1
Bn=1)のときは、
An, Bnのどちらか一方は1なので、Cn-1=1ならばCn=1、つまりCn = Cn-1
EXORやセレクタに上記のような回路を使うとして、
全部で何個のMOSFETが必要か、考えてみましょう。
(答え: 22個)
マンチェスタ・キャリー連鎖 (MCC)
ちょっと趣向を変えて、桁上げ伝播加算器の構成で、
桁上げの伝播だけを速くする方法について考えてみることにしましょう。
CLAのところで導いたように、Cnは次の式のように書くことができます。
これを、次のような回路で作ってみることにしましょう。
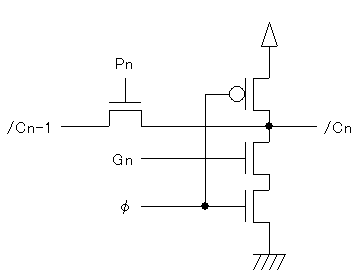
このような回路は、動作を理解するのにちょっとコツがいります。
次のような順で考えるとよいでしょう。
- まずφ=0とする(プリチャージ)→/Cnに電荷がたまり、/Cn=1となる
- 次に、φ=1とする。このとき、
- Gn = 1ならば、/Cnにたまった電荷が放電され、/Cn=0となる
- Pn = 1ならば、/Cn-1=0のときには、/Cn=0となる
つまりCn = Gn + Pn・Cn-1という式そのものの動作をしているわけです。
ポイントは、まずは最初にφ=0とするプリチャージをしてから、
Cnの値を求める(評価する)必要がある、ということです。
このようにプリチャージが必要な回路をダイナミック回路と呼びますが、
動作のたびにプリチャージが必要な反面、必要なトランジスタ数が
少なくて済むという利点があります。
さてこれをどんどんつなげていくと、桁上げの伝播だけ
求めることができる、次のような回路ができます。(これは4ビットの場合)
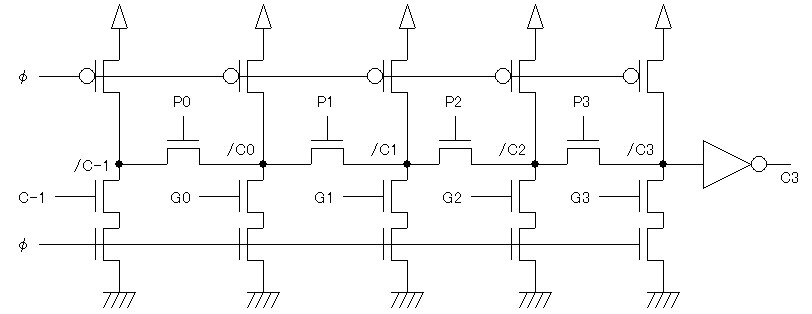
このような回路をマンチェスタ・キャリー連鎖 (Manchester Carry Chain)と
呼びます。
この回のソボクな疑問集
戻る
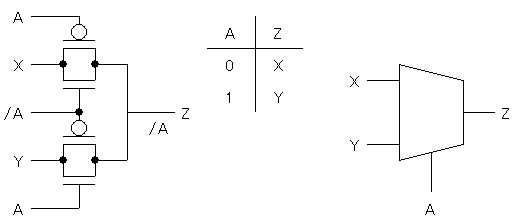




 Bn=0)のときは、Sn = Cn-1
Bn=0)のときは、Sn = Cn-1
 Bn=1)のときは、Sn = /Cn-1
Bn=1)のときは、Sn = /Cn-1
 Bn=0)のときは、
An=Bn=1ならばCn=1、An=Bn=0ならばCn=0、つまりCn=Bn ( =An)
Bn=0)のときは、
An=Bn=1ならばCn=1、An=Bn=0ならばCn=0、つまりCn=Bn ( =An)
 Bn=1)のときは、
An, Bnのどちらか一方は1なので、Cn-1=1ならばCn=1、つまりCn = Cn-1
Bn=1)のときは、
An, Bnのどちらか一方は1なので、Cn-1=1ならばCn=1、つまりCn = Cn-1

