第9回: 乗算器(その2)

ブースのアルゴリズムの例

まずX, Yを2進数で求めると次のようになります。

• X = 11 0111 = x₅x₄x₃x₂x₁x₀
• Y = 01 1001 = y₅y₄y₃y₂y₁y₀

Z0 =                  11111110111 (11桁にあわせる)
Z1 = -2・  11011100 = 00001001000 (11桁にあわせる)
Z2 =  2・1101110000 = 11011100000
----------------------------------
                      11100011111

ブースのアルゴリズムを使った乗算器の設計

ブースのアルゴリズムによるQ1, Q2, QNの生成

y(2j+1) y(2j) y(2j-1) Y(j) | Q1 Q2 QN
---------------------------+---------
  0       0      0     0   |  0  0  0
  0       0      1     1   |  1  0  0
  0       1      0     1   |  1  0  0
  0       1      1     2   |  0  1  0
  1       0      0    -2   |  0  1  1
  1       0      1    -1   |  1  0  1
  1       1      0    -1   |  1  0  1
  1       1      1     0   |  0  0  0

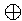• Q1 = y_2jy_2-1
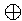• Q2 = (y_2j+1y_2j)・/(y_2j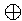y_2j-1)
• QN = y_2j+1・/(y_2j・y_2j-1)

部分積Z_jの生成

• Z_j = X・Y_j・2^2j

• Z = Σ_j=0^(N-2)/2Z_j

• Z_j = (-1・A_Nj・2^N + Σ_i=0^N-1A_ij・2ⁱ + C_j)・2^2j

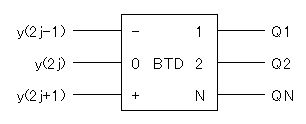
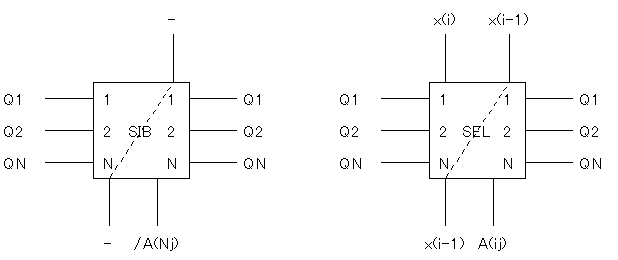
まずA_Njは符号ですから、QN=0のときにはZ_jの符号はXの符号と同じであり、 逆にQN=1のときにはY_jが負となるためにXの符号を反転させる必要があります。

同様に、Q1=1のときにはXを2jビットシフトさせるのですが、 このZ_jの式には、2jビットシフトさせる2^2jがすでにありますから、 i桁目、つまりA_ijは、Xのi桁目x_iと同じになります。 しかしQ2=1のときには、Xを(2j+1)ビットシフトさせる必要があるので、 結果としてi桁目のA_ijは、Xの(i-1)桁目x_i-1と同じになります。

さらにQN=1のとには、A_ijを求めるのに 2の補数をとらなければなりませんから、A_ijを反転させ(1の補数)、 全体に1を加える必要があります。

以上から、Q1, Q2, QNとA_Nj, A_ij, C_jは 次のような関係になるでしょう。

Q1	Q2	QN	ANj	Aij	Cj
0	0	0	0	0	0
1	0	0	xN-1	xi	0
0	1	0	xN-1	xi-1	0
0	1	1	/xN-1	/xi-1	1
1	0	1	/xN-1	/xi	1

これから、A_Nj, A_ij, C_jは次のような論理式になるでしょう。

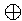• A_Nj = /{ /(Q1 + Q2) + /(QNx_N-1) }
• A_ij = /{ /(Q1・x_i)・/(Q2・x_i-1) } QN
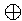• C_j = QN