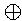 Bn
Bn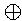 Cn-1
Cn-1
1桁の2進数、とは、0か1か、ですから、2つの1桁2進数の加算、は、 次の4通りしかありません。
A B | C S ----+---- 0 0 | 0 0 0 1 | 0 1 1 0 | 0 1 1 1 | 1 0この真理値表を満たす論理回路こそ、「1ビットの加算器」であるわけです。 このような加算器を半加算器 (half adder; HA)と呼びますが、 実はこの半加算器だけでは、桁数の多い加算を行うことができません。 たとえば次のような2桁の加算を行うことを考えましょう。
0 1 +) 1 1 ------ 1 0 0一番下の桁の加算の結果、上の桁に桁上がり1があって、 上の桁では、この下の桁からの繰り上がりと、与えられている0, 1の加算、 つまり結果として 1 + 0 + 1 = 10 という、3つの数の加算を 行っているわけです。 半加算器は2つの数の加算を行うだけでしたから、 これではまずいわけです。
そこで、3つの数の加算を行う加算器を考えることにしましょう。 つまり次のような真理値表を考えるわけです。
An Bn Cn-1 | Cn Sn -----------+------ 0 0 0 | 0 0 0 0 1 | 0 1 0 1 0 | 0 1 0 1 1 | 1 0 1 0 0 | 0 1 1 0 1 | 1 0 1 1 0 | 1 0 1 1 1 | 1 1このような真理値表を持つ論理回路を 全加算器 (full adder; FA)と呼びます。 これは、n桁目のAn, Bnと、下の桁(n-1桁目)からの桁上がり信号Cn-1を 加算する、というはたらきです。 そして結果のCnが、このn桁目で発生する桁上がり、つまり次のn+1桁目へ 渡される桁上がり信号であるわけです。
この全加算器の作り方はいろいろあります。 たとえば地道に真理値表からカルノー図を描いて論理関数を簡略化して 論理回路を作る方法、2つの半加算器を組み合わせる方法(下図)、 などです。 (この方法は、「A+B+C = (A+B)+Cと分け、A+Bか(A+B)+Cのどちらかで 桁上がりが起こると、全体として桁上がりが起こる、ということを 使っているわけです)
+----+ ORゲート
An ---| C|-------------)--
| HA | +----+ ) >-- Cn
Bn ---| S|----| C|---)--
+----+ | HA |
Cn-1 -------------| S|---------- Sn
+----+
このうち、
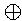 Bn
Bn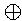 Cn-1
Cn-1
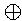 Bn (伝播項)
Bn (伝播項)
 リプルキャリー加算器では、前の桁の桁上げ(キャリー)が
次の桁の入力につながっていますので、最大ですべての桁、つまり
桁数分(=N)のキャリーの伝播が起こることになり、
全体として加算が終了するまでの時間(演算時間)は
桁数Nに比例する、という問題点があります。
リプルキャリー加算器では、前の桁の桁上げ(キャリー)が
次の桁の入力につながっていますので、最大ですべての桁、つまり
桁数分(=N)のキャリーの伝播が起こることになり、
全体として加算が終了するまでの時間(演算時間)は
桁数Nに比例する、という問題点があります。
 Bn (伝播項)
Bn (伝播項)
たとえば4ビット加算器をつくるとして、 この生成項と伝播項を順番に書くと次のようになります。
| G0 = A0・B0 | Q0 = A0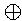 B0 B0 |
C0 = G0 + Q0・C-1 |
| G1 = A1・B1 | Q1 = A1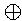 B1 B1 |
C1 = G1 + Q1・C0 |
| G2 = A2・B2 | Q2 = A2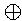 B2 B2 |
C2 = G2 + Q2・C1 |
| G3 = A3・B3 | Q3 = A3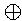 B3 B3 |
C3 = G3 + Q3・C2 |
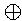 B1){A0・B0 + (A0
B1){A0・B0 + (A0 B0)・C-1}
B0)・C-1}
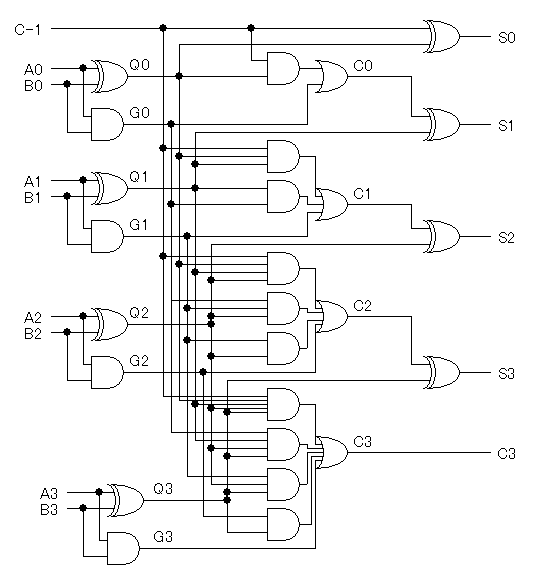
このようにCLAは桁数が多くても高速な演算が可能ですが、 桁数が多くなるほど、キャリーCnを求めるための論理式が 急激に複雑になり、論理回路が大規模になってしまうという問題があります。 (元気がある人は8ビットCLAでも作ってみましょう・・・) 現実的にはCLAの構成は4ビット分にとどめ、それ以上のビット数の 加算器が必要な場合は、4ビットCLAをつなげる、という構成をとるのが 一般的です。