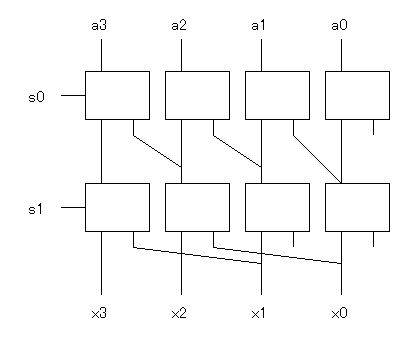
この図は、4ビットの2進数[a3:a0]を、右に[s1:s0]ビット分(2進数表現) シフトした結果[x3:x0]を求めるためのバレルシフタの回路です。 □ブロックはセレクタを表します。
| 数(1) | 1の補数 | 2の補数(2) | (1)+(2) |
| 000 | 111 | (1)000 | (1)000 |
| 001 | 110 | 111 | (1)000 |
| 010 | 101 | 110 | (1)000 |
| 011 | 100 | 101 | (1)000 |
| 100 | 011 | 100 | (1)000 |
| 101 | 010 | 011 | (1)000 |
| 110 | 001 | 010 | (1)000 |
| 111 | 000 | 001 | (1)000 |
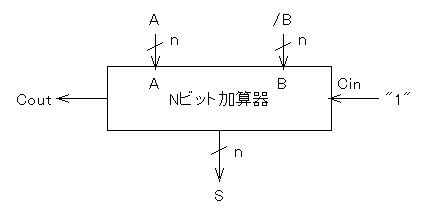この2の補数を使うと、減算を行う減算器を作ることができます。
つまりこのようにN桁の加算器で、最下位の桁上がり入力Cinを
使うと、S = A + B + Cin ということですが、
たとえばBのところに/B(つまりBの全ビットの反転をとったもの)を
入力し、Cin=1とすれば、S = A + (/B + 1) となりますが、
「/B+1」は、Bの2の補数そのものですから、結果としてS = A - B を
求めたのと同じことになります。
| S1 | S0 | B | Cin | S = A + B + Cin | 内容 |
| 0 | 0 | すべて0 | 0 | A | そのまま |
| 0 | 0 | すべて0 | 1 | A+1 | increment |
| 0 | 1 | B | 0 | A+B | 加算 |
| 0 | 1 | B | 1 | A+B+1 | |
| 1 | 0 | /B | 0 | A+/B | |
| 1 | 0 | /B | 1 | A+/B+1 = A-B | 減算 |
| 1 | 1 | すべて1 | 0 | A -1 | decrement |
| 1 | 1 | すべて1 | 1 | A |
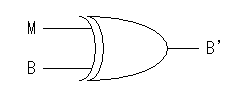
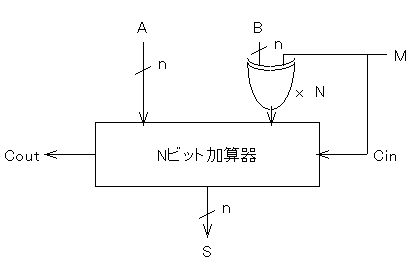
このような種々の算術演算(加算・減算など。乗算・除算は除く)に加えて、 論理演算、すなわちビットごとの論理積(AND)・論理和(OR)・否定(NOT) ・排他的論理和(EXOR)を、機能を切り替えて演算できる回路を 作ることができます。 このような回路を、算術論理演算ユニット(Arithmetic Logic Unit; ALU)と 呼びます。
論理演算の一種に「シフト演算」があります。 これは、C言語で「>>」や「<<」という演算子であらわす演算で、 2進数としての変数の値を、全体に右あるいは左にシフトするものです。 (シフトしてあいたビットに入れる値によって、論理シフトと算術シフトの 2種類がある) このシフト演算は、例えば2n倍の乗算に使えたりと、 いろいろと使える場面が多いので、専用の演算回路として持っている プロセッサ(特にDSP)も多いようです。
シフト演算回路(シフタ)の構成にもいくつかありますが、
最も効率のよい回路として「バレルシフタ」と呼ばれるものが
知られています。
この図は、4ビットの2進数[a3:a0]を、右に[s1:s0]ビット分(2進数表現)
シフトした結果[x3:x0]を求めるためのバレルシフタの回路です。
□ブロックはセレクタを表します。
バレルシフタでは、このように1ビット, 2ビット, 4ビット, ・・・という 2nのシフトを行うか行わないかを、 1段ごとのセレクタで選択し、実際の「シフト」は、2nビット分 シフトした先に配線がつながっていることで行われていることになります。 左シフトや算術シフトも同様に構成することができます。