1つは「ナレータ」と呼ばれるもので、 両端の電圧が常にゼロで、流れる電流も常にゼロとなる、という素子です。
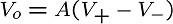
ここで、さらに、次のような特性を仮定することにします。
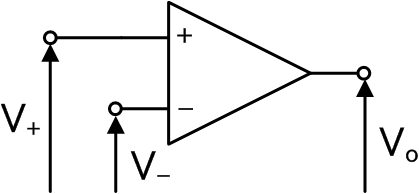
実はこの仮定から、オペアンプの大切な性質が導かれます。 それは「常にV+=V-」となるというものです。 なぜならば、仮に「V+とV-が等しくない」とすると、 Vo = A(V+ - V-)で、V+ - V-はゼロではありませんから、 A=∞という性質から、Voも無限大となってしまいます。 ところが増幅器ではVo=∞というのはありえない(はず)なので、 この前提が間違っていた、つまりV+=V-である、というわけです。 (いわゆる背理法)
このような理想オペアンプを含む回路の特性を考えるときに、
次のような2つの仮想的な素子を考えるととても楽ですので
紹介しておきましょう。

1つは「ナレータ」と呼ばれるもので、
両端の電圧が常にゼロで、流れる電流も常にゼロとなる、という素子です。
もう1つは、名前が似ているのですが「ノレータ」と呼ばれるもので、 逆に両端の電圧も流れる電流も、いくらでもかまいません。
このナレータとノレータは、抵抗に似ているようが気がするかもしれませんが、 抵抗だと、常にV=IRという関係がありますので、 常に電流が流れないナレータは、R=∞のはずですが、 両端の電圧がつねにゼロですから、抵抗ではありません。 逆にノレータも、両端電圧と流れる電流が、両方ともどのような値でも よいので、R=V/Iが一定とならず、やはり普通の抵抗ではありません。
このようなナレータとノレータを使うと、理想オペアンプの中身は
次のように考えればよいでしょう。

つまり2つの入力端子に電圧差がなくて電流が流れないことを
ナレータであらわし、出力の電圧や電流が好きに決まることを
ノレータであらわしているわけです。
この理想オペアンプの中身の回路(等価回路)は、
後で使うことにしましょう。

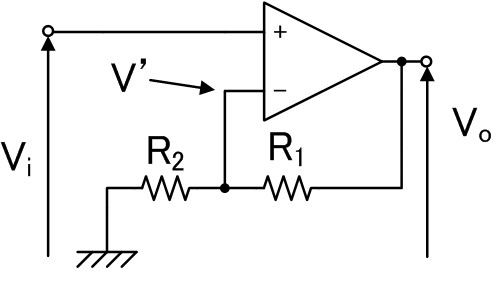
このような回路の、入力Viと出力Voの関係(特性)を求めてみます。
まず理想オペアンプという仮定から、-側の電圧V'は、+側の電圧(=0V)と
等しくなります。
したがて抵抗R1の両端電圧はViですので、そこに流れる電流は
Vi/R1となります。
ところが理想オペアンプの入力端子には電流が流れませんから、
この電流はすべてそのまま抵抗R2に流れていきます。
すると抵抗R2の両端の電圧は、「この流れる電流」×R2、
つまり(R2/R2)Viとなりますが、抵抗R2の左側の電圧が0Vですから、
右側の電圧は、0-(R2/R1)Vi=-(R2/R1)Viとなりますが、これは
出力電圧Voそのものです。
つまり次のような関係ということになります。
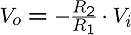
このように、この回路の出力は、入力をR2/R1倍に増幅し、
かつ符号が逆になりますので、反転増幅回路と呼ばれます
この反転増幅回路は非常に応用範囲が広いので、また後で 触れることにしましょう。