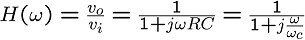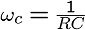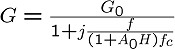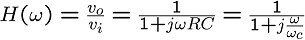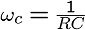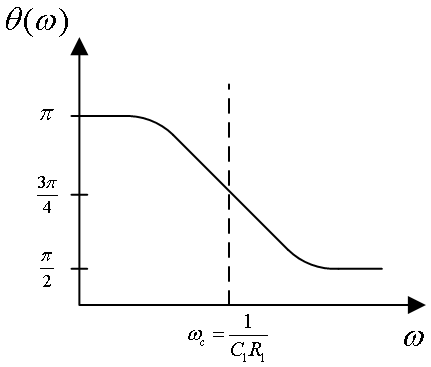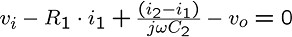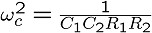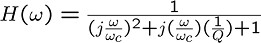第3回: オペアンプ(その2)

負帰還の理論

一般に、「出力の一部を、入力に戻す」回路を帰還回路と 呼びますが、特に「出力の一部を、マイナスにして入力に戻す」 回路を負帰還回路と呼びます。



負帰還回路はこの図のようにモデル化できます。 図中のそれぞれのパラメータは次のとおりです。 つまり出力をH倍に減衰させて、入力Vinから引いているわけです。 したがって次のような関係が成り立ちます。






この2つの式からViを消去すると、VoとVinの比、 つまり全体伝達特性Gは次のようになります。




ところが一般的には、Aは非常に大きいため、 AH>>1と近似することができます。 したがって伝達特性Gは、次のようになります。




つまり全体の伝達特性(つまり増幅率)は、 「Aが何倍か」には関係なく、 「1/H倍」になるわけです。 一般にHは抵抗での分圧で作ることが多く、 その値は非常に正確になります。 したがって全体の伝達特性も、非常に正確にできるわけです。

オペアンプは「Aが十分大きい(理想的には無限大)」増幅器で、 かつ2つの入力のうち片方がマイナスになっていますので、 オペアンプを使った回路は、まさに「負帰還」を使った回路であるわけです。

負帰還回路と増幅器の周波数特性

※講義では触れていません


一般に増幅器の増幅率Aは、ある周波数fcより 高い周波数では、周波数に比例して増幅率が 低下していきます。 つまり増幅率Aは、次のような式で書けることになります。 (1次のRC回路と同じですね)




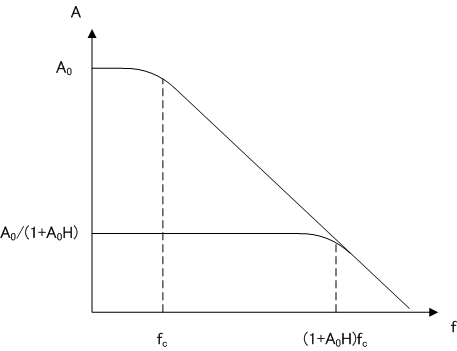
これを、前回の負帰還増幅回路の伝達特性Gの式に代入すると、 次のようになります。




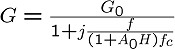
ただしG0 = A0 / (1 + A・H)です。

この式から、この負帰還増幅回路の増幅率が下がり始める 周波数は、(1 + A0・H)fc、つまり(1 + A0・H)倍と 増えます。 ただし直流(f=0)での増幅率は A0 / (1+A0・H) 倍と A0よりも小さくなりますので、 結果として 「直流で増幅率を下げた分、高い周波数まで増幅できる回路」 ができることになります。

受動フィルタ(復習)

今回は、ある一定の周波数の信号のみを通す「フィルタ(filter)」回路を オペアンプをつかってつくることを考えていきましょう。 まずは前期の情報回路第1の復習から入りましょう。

RC 1次フィルタ



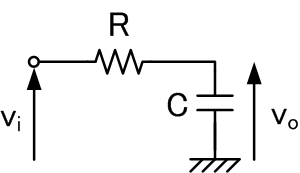
この図のようにRとCからなる回路の、入力viと出力voの比、 すなわち伝達関数H(ω)を求めてみます。 といってもコンデンサのインピーダンスが入力の周波数(or角周波数ω)によって 変わりますから、このH(ω)もωによって変わる、すなわちωの関数となります。

回路方程式(というほどのものでもないが・・・)を解いてみると、 次の式が導かれるでしょう。



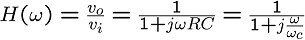
ただし



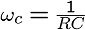
分母にωの1次式が入っているため、「1次の(ローパス)フィルタ」と呼ばれます。

オペアンプを使った1次フィルタ

前回は、いきなり複雑なフィルタを紹介してしまいましたので、 今回はちょっと戻って、オペアンプを使った1次のフィルタみましょう。


このような回路の伝達関数を、反転増幅器のときと同じように求めると 次のようになります。



つまり、1次のLPF、ということになります。 ただし全体の増幅率がR2/R1ですから、RCだけからなる受動フィルタと違い、 増幅もいっしょにできる、という特性があります。 ちなみにこれのボード線図は次のようになるでしょう。

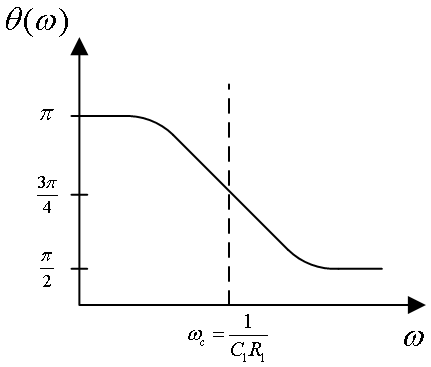
オペアンプを使ったフィルタ(その1: VCVS型)



オペアンプを使って、フィルタ回路をつくることを考えましょう。 やや天下り的ではありますが、この図のような回路を考えてみます。 この回路の、伝達関数H(ω)=vo/viを求めたいわけですが、 地道にやっていくことにしましょう。 ※講義中には別の導き方を紹介しました。


この図のような等価回路を描いてみます。 (2つの入力の電圧が同じで電流が流れない、などで、等価的に同じことを 考えています) 次のような式が導かれるでしょうか。




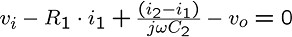
※[訂正]第1式の第3項の分母のC2は、正しくはC1です
最初の式に、最後の式を i2 = jωC2・vo と変形してから 代入すると、



となりますので、これを２番目の式に代入すると、 最終的に次のような式が導かれます。



かなり見にくい式ですので、




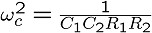
とおいてみると、 次のように書くことができます。



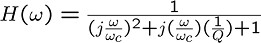
これは、LC2次LPFの伝達関数(次回資料参照)そのものですから、 このオペアンプの回路も、2次のLPFであることがわかります。 オペアンプを使ったこの形のフィルタを、 VCVS型 (voltage Controlled voltage Source型)と呼びます。

両方とも同じ伝達関数ならオペアンプをわざわざ使う必要はない、という 気もしますが、 周波数が低いところで使うフィルタを作ろうとすると、 特性のよいインダクタ(直列抵抗が小さいもの)を作るのが困難であるため、 一般に、周波数が高いところで使うフィルタを作るときにはLC回路で、 周波数が低いところで使うフィルタを作るとき、またはフィルタ自身に 増幅性能を持たせたい(この回路ではできませんが、オペアンプを 使っていますから、増幅性能を持たせることは可能です)ときには、 オペアンプを使ったフィルタ(能動フィルタ)を使うことが 多いようです。

この回のソボクな疑問集
戻る