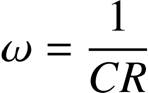一般に、出力の一部を入力に戻す回路を帰還回路と呼び、
その例として、第1回のときに負帰還回路の紹介をしました。
この帰還回路をうまく作ると、入力を与えなくても
出力が出てくるような回路をつくることができます。
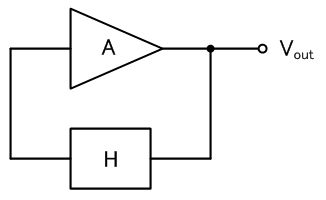
この図のように、A倍の増幅器の出力Vout を、さらにH倍して増幅器に戻すような回路を考えてみましょう。
このとき、VoutがH倍された後で増幅器でA倍され、再びVout になるわけですから、
この一回り(ループ)で、Vout はAH倍されることになります。
このAHをループ利得と呼びます。
一般にHは周波数ω によって変わりますから、 逆に言うと、このような回路では、この2つの条件をみたすような周波数の信号に対しては、この周波数のVout 、 つまり周波数ω の正弦波が常に出続けることになります。
ちなみにこれ以外の周波数では一般に Re(AH) < 1 となりますが、
これはVout が、ループを一回りすると小さくなってしまうわけですから、
次第に0に集束してしまい、この周波数の信号は現れなくなってしまうことになります。
したがって、この2つの条件を満たすような周波数ωの信号(正弦波)のみがVout として現れることになります。
このような回路を発振回路と呼びます。

この図のような、オペアンプを使った回路を考えてみましょう。
この回路をウイーンブリッジ発振回路(Wien Bridge Oscillator)と呼びますが、その名のとおり、実は発振回路になっています。

残りの部分は、次の図のように、出力電圧Vout から、抵抗とコンデンサの回路を通して、オペアンプの+端子側の電圧V+ 、つまり非反転増幅回路の入力電圧を決めているわけです。


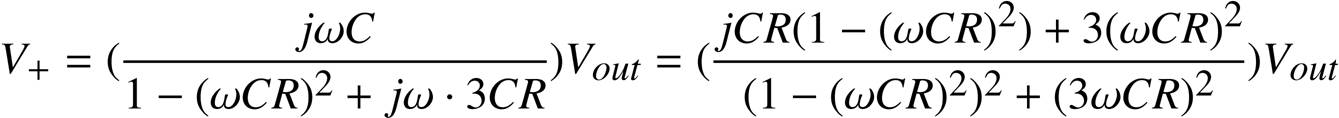
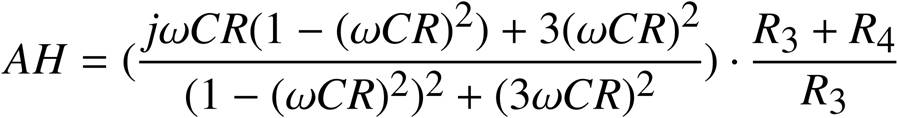
![]()
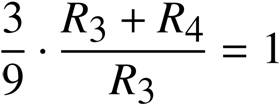 から
から