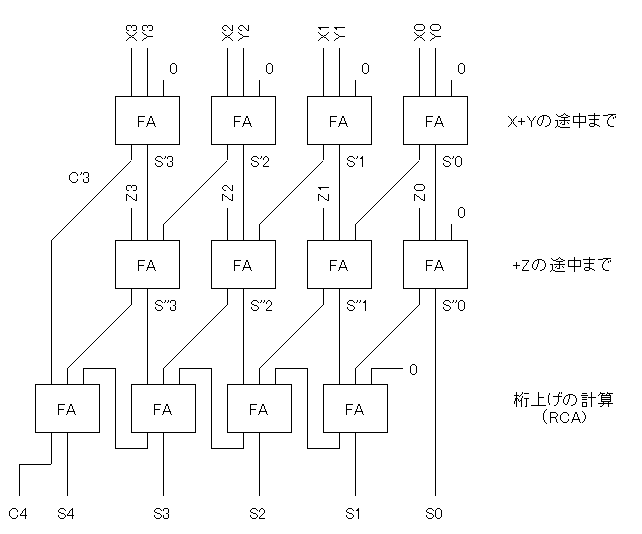

※RCAのMOSFET数が妙に多いように見えますが、 この「MOSFET数」は、標準サイズのMOSFETに換算した数です。 (つまり実際のLSI上で占める面積の目安) 高速化するためにMOSFETの大きさを大きくしないといけない部分が 多く、MOSFETの数自体は少ないものの、この換算した「MOSFET数」は 多くなるわけです。
| 数(1) | 1の補数 | 2の補数(2) | (1)+(2) |
| 000 | 111 | (1)000 | (1)000 |
| 001 | 110 | 111 | (1)000 |
| 010 | 101 | 110 | (1)000 |
| 011 | 100 | 101 | (1)000 |
| 100 | 011 | 100 | (1)000 |
| 101 | 010 | 011 | (1)000 |
| 110 | 001 | 010 | (1)000 |
| 111 | 000 | 001 | (1)000 |
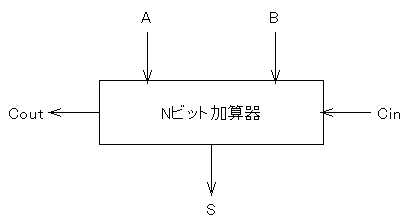 この2の補数を使うと、減算を行う減算器を作ることができます。
つまりこのようにN桁の加算器で、最下位の桁上がり入力Cinを
使うと、S = A + B + Cin ということですが、
たとえばBのところに/B(つまりBの全ビットの反転をとったもの)を
入力し、Cin=1とすれば、S = A + (/B + 1) となりますが、
「/B+1」は、Bの2の補数そのものですから、結果としてS = A - B を
求めたのと同じことになります。
この2の補数を使うと、減算を行う減算器を作ることができます。
つまりこのようにN桁の加算器で、最下位の桁上がり入力Cinを
使うと、S = A + B + Cin ということですが、
たとえばBのところに/B(つまりBの全ビットの反転をとったもの)を
入力し、Cin=1とすれば、S = A + (/B + 1) となりますが、
「/B+1」は、Bの2の補数そのものですから、結果としてS = A - B を
求めたのと同じことになります。
このように拡張していくと、B, Cinに与える値によって 次の8通りの演算ができることがわかります。
| S1 | S0 | B | Cin | S = A + B + Cin | 内容 |
| 0 | 0 | すべて0 | 0 | A | そのまま |
| 0 | 0 | すべて0 | 1 | A+1 | increment |
| 0 | 1 | B | 0 | A+B | 加算 |
| 0 | 1 | B | 1 | A+B+1 | |
| 1 | 0 | /B | 0 | A+/B | |
| 1 | 0 | /B | 1 | A+/B+1 = A-B | 減算 |
| 1 | 1 | すべて1 | 0 | A -1 | decrement |
| 1 | 1 | すべて1 | 1 | A |
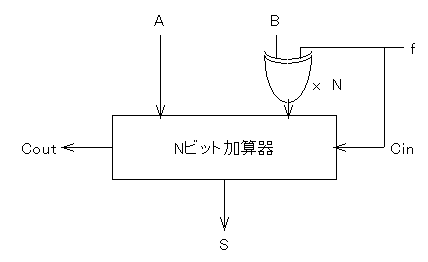
 ちなみにBのところは、上のような回路(EXORゲートそのもの)を入れておけば、
f=0のときはBが、f=1のときは/Bが、加算器に与えられることになりますから、
fの値に応じて加算(f=0)と減算(f=1)を切り替えるためには
次のような回路とすればよいでしょう。
ちなみにBのところは、上のような回路(EXORゲートそのもの)を入れておけば、
f=0のときはBが、f=1のときは/Bが、加算器に与えられることになりますから、
fの値に応じて加算(f=0)と減算(f=1)を切り替えるためには
次のような回路とすればよいでしょう。
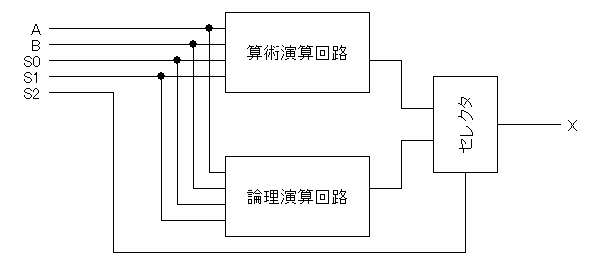
 このように、いろいろな演算機能をもつ演算ユニットを総称して
算術論理演算ユニット (Arithmetic Logic Unit; ALU)と
呼びますが、この回路は、加算と減算機能をもつALU、ということになります。
このように、いろいろな演算機能をもつ演算ユニットを総称して
算術論理演算ユニット (Arithmetic Logic Unit; ALU)と
呼びますが、この回路は、加算と減算機能をもつALU、ということになります。
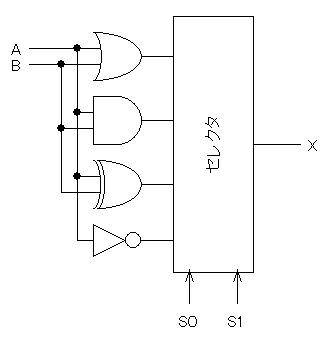
ただ、これはあまり格好いい回路とはいえません。 そこで、このALUの真理値表を書いてみることにしましょう。
A | 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1
B | 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1
S1 | 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
S0 | 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
---+---------------------------------------
X | 0 1 1 1 0 0 0 1 0 1 1 0 1 0 1 0
(OR) (AND) (EXOR) (NOT)
そしてこの真理値表から、積和標準形やカルノー図などを用いて論理式を
つくり、それから論理回路をつくれば、所望の論理演算ユニットを
つくることができます。
(つまり入力がA, B, S1, S0の4変数で、出力がXの論理式)